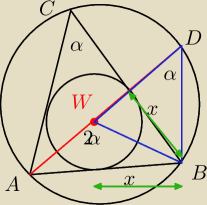
planimetria salamandra: Punkt W jest środkiem okręgu wpisanego w trójkąt ABC. Prosta przechodząca przez punkty A i W przecina okrąg opisany na trójkącie ABC w punkcie D. Wykaż, że trójkąt BDW jest równoramienny. Ustaliłem jedynie, że "x" są równe jako odcinki styczne, kąt ACB i ADB kąty wpisane oparte na łuku AB, AWB kąt środkowy oparty na łuku AB, kąt DWB to będzie 180−2α i kąt DBW w tym momencie to 180−α−(180−2α)=α, więc DWB równoramienny, bo ma dwa kąty α przy podstawie DB

ite: A gdzie jest na rysunku środek okręgu opisanego na ΔABC?

salamandra: o kurde, zagalapowałem się

salamandra: zagalopowałem* to nie wiem w takim razie jak to ugryźć z błędnego rozwiązania tak pięknie wyszło, ale faktycznie, to jest środek okręgu wpisanego a nie opisanego

Maciess: Ile wynosi miara kąta BWD? Ile w takim razie miara kąta WBD? Co jeśli trójkąt ma dwa takie same kąty? Koniec zadania

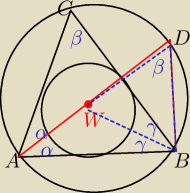
salamandra: Zmienię koncepcję, może z tego "coś" wyjdzie teraz zauważyłem, że skoro prosta AD przechodzi przez środek okręgu wpisanego "W", to musi dzielić kąt BAC na dwa równe kąty, jako że środek leży na przecięciu się dwusiecznych. Analogicznie prosta BW też podzieli na dwa kąty γ

f123: @salamandra z definicji srodek okregu wpisanego w trojkat lezy na przecieciu jego dwusiecznych katow

salamandra: no zastosowałem to jak widzisz, ale nadal nie wiem jak "dopiąć"

f123: @salamandra juz patrze na tresc zadania, moze cos podpowiem

Maciess: Na pierwszym rysunku masz wszystko. Przeczytaj co ci napisalem

ite: Ile ma <DWB ?

salamandra: No właśnie Maciess przeczytałem, ale nie widzę jak znaleźć ten BWD

f123: @salamandra przypomnij sobie katy wpisane w okrag, a katy srodkowe

Eta: https://matematykaszkolna.pl/forum/345269.html

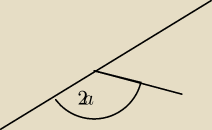
Maciess: Do ilu sumują się kąty przyległe?

f123: sorry, jednak nie, farmazona strzelilem, myslalem ze W jest to srodek okregu opisanego na trojkacie

salamandra: @f123, przecież trójkąt DBW nie jest wpisany w okrąg

salamandra: Ja też ten błąd popełniłem jak widac po moim pierwotnym rozwiązaniu

salamandra: Maciess, problem w tym, że tam nie ma 2α.

Maciess: A to pardon

f123: @salamandra mam juz rozwiazanie, zaraz ci tu je przepisze

salamandra: Nie musisz, Eta kiedyś tam dokończyła dzieki

f123: kat BCA = 180 −2α − 2β Trojkat ACE (E − punkt przeciecie sie srodkowej z obkiem trojkata) kat CEA = 3α − 2β = kat BED Trojkat BWD kat BWD = α + β kat BDW = kat BCA (katy wpisane w okrag, oparte na tym samym luku) = 180 − 2α − 2β Trojkat BED kat EBD = α Trojkat BWD kat WBD = α + β kat BWD = α + β kat BDW = kat BCA (katy wpisane w okrag, oparte na tym samym luku) = 180 − 2α − 2β

f123: @salamandra za pozno

Eta: