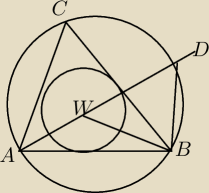
Planimetria KML: Punkt W jest srodkiem okregu wpisanego w trojkąt ABC. Prosta przexhodzaca przez punkty A i W przecina okrąg opisany na trojkącie Abc w punkcie D. Wykaz , ze trojkat BDW jest równoramienny.

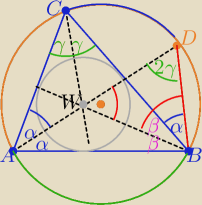
Eta: Środek W leży w punkcie przecięcia dwusiecznych kątów trujkąta ABC to 2α+2β+2γ=180^o ⇒ α+β+γ=90^o ⇒ α+β= 90^o−γ i z własności kątów wpisanych w duży okrąg W ΔBWD |<BWD|= 180^o−(|<WBD|+|<WDB|)= ..... = 90^o−γ zatem ΔWBD jest równoramienny o ramionach |WD|=|BD|

Adam: trujkąt

Adam: dowód bardzo ładny

Eta: trójkąt ( może będę "prezydentem " w bólu

salamandra: Eta, moglbym jeszcze dopytać skąd u Ciebie się wziął kąt α przy wierzchołku B?

Eta: To kąty wpisane oparte na łuku CD = α

salamandra: a no tak