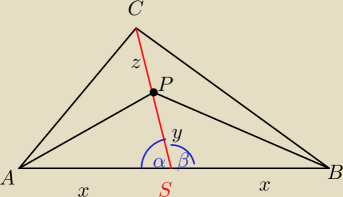
planimetria salamandra: Punkt P należy do środkowej CS trójkąta ABC. Uzasadnij, że pola trójkątów APC i PBC są równe. β=180−α

	1
PASC=PSBC, bo PASC=		*(z+y)*sinα, a
	2

	1		1
PSBC=		*(z+y)*sin(180−α)=		*(z+y)*sinα
	2		2

P_ASP i P_PSB również równe na tej samej zasadzie, ale jak udowodnić dla APC i PBC?

wredulus_pospolitus: Straszne rzeczy piszesz wystarczy narysować H (z wierzchołka C) i h (z wierzchołka P) I mamy:

	x*H
PASC =		= PBSC
	2

	x*h
PASP =		= PBSP
	2

więc: P_APC = P_ASC − P_ASP = P_BSC − P_BSP = P_BPC

wredulus_pospolitus: Nie mówić już o tym, że można się powołać na twierdzenie że środkowa dzieli pole trójkąta na dwa równe pola.

Saizou : To analogiczne zadanie. Niech dany będzie trapez ABCD oraz niech P będzie punktem przecięcia się jego przekątnych. Uzasadnić, że P_ASD=P_BSC.

ICSP: P_ASC = P_BSC P_ASP + P_APC = P_BCP + P_BPC ponieważ P_ASP = P_BSP to P_APC = P_BPC a to jest własnie teza.

f123: A wiec: P_ASP + P_APC = P_ASC P_SBP + P_BPC = P_SBC P_ASC = P_SBC P_ASP = P_SBP P_SBP + P_BPC = P_ASP + P_APC ⇒ P_APC = P_BPC

salamandra: ależ ja głupi, przecież od tego ACS mogę odjąć ASP co wyliczyłem i mam APC

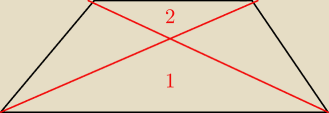
salamandra: @Saizou pamiętam jak Eta lub Mila gotowy wzór na coś podobnego podawały, ale to było bodajże dla takiej sytuacji że P_trapezu=√P₁²+P₂² bodajże?

f123: A na maturze mozna korzystac z gotowych wzorow, ktore nie sa w karcie wzorow maturalnych? Czy trzeba je wyprowadzac jak w fizyce?

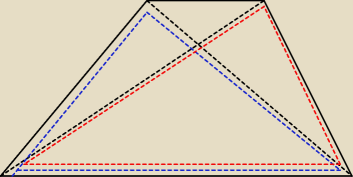
wredulus_pospolitus: rozpatrz pola czerwonego i niebieskiego trójkąta. A następnie odejmij pole 'części wspólnej'

salamandra: To wtedy będę miał pole dwóch małych, a jak udowodnić ze są one równe?

wredulus_pospolitus: udowodnisz od wykazania, że czerwpny i niebieski mają równe pola ... a jak to udowodnić

wredulus_pospolitus: dowodzisz to od wykazania*

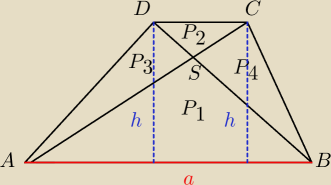
Saizou : P_ABC=P_ABD zapisz to za pomocą P₁, itd.

salamandra: no łatwo, bo wysokość będzie wspólna i podstawa również

salamandra: P_ABC=P₁+P₃ P_ABD=P₁+P₄ P₁+P₃=P₁+P₄ P₃=P₄

Saizou :

salamandra: Pamiętacie ten wzór na pole trapezu znając P₁ oraz P₂, czy musimy poczekać na którąś z Pań?

Saizou : https://matematykaszkolna.pl/forum/319132.html

salamandra: