stereo
jaros:
| | 1 | |
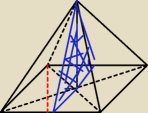
podstawą ostrosłupa jest romb którego bok ma długość 8 |
| a jedna z przekątnych ma długość |
| | 3 | |
| | 1 | |
13 |
| . Spodek wysokości ostrosłupa jest środkiem symetrii podstawy. Przekrój tego |
| | 3 | |
ostrosłupa wyznaczony przez wysokości przeciwległych ścian bocznych jest trójkątem
równobocznym. Wyznacz pole tego przekroju.
| | 200 | |
Doszedłem do tego momentu, iż wyznaczyłem wysokość rombu = 8, pole rombu = |
| 2 |
| | 3 | |
przekątna = 10, ktoś "popchnie" mnie dalej?
26 mar 19:14
f123: Niestety jeszcze nie znalazlem rozwiazania..Przy okazji skad takie zadanie wytrzasnales

?
26 mar 19:36
ite: Będę się poruszać w odwrotną stronę:
→ Na końcu drogi jest cel = obliczenie pola przekroju, który jest trójkątem równobocznym. Co
trzeba wiedzieć, żeby policzyć to pole? Trzeba znać np. bok lub wysokość tego trójkąta.
→ No to szukamy boku trójkąta. Czemu jest równy? Wysokości rombu, który jest podstawą
ostrosłupa.
→ I już jest do wykorzystania wysokość rombu, a to masz policzone.
26 mar 19:44
ite: Tak dla wprawy narysuj ścianę boczną i zaznacz na niej wysokość,
narysuj podstawę ostrosłupa i zaznacz na niej bok trójkąta, który jest przekrojem.
Bo na Twoim rysunku coś jest nie tak.
26 mar 19:48
jaros: @f123 kurczab − stereo
26 mar 19:48
jaros: Hmmm wiemy to dlatego, że w nie bez powodu jest tam informacja o tym, że "Spodek wysokości
ostrosłupa jest środkiem symetrii podstawy" czyli jeżeli jedna część obrócimy o 180 stopni to
dostaniemy pokrywającą się z nią górną część. więc....

? nie mam bladego pojęcia o czym mi to
mówi xD
26 mar 19:52
f123: @ite skad taka mysl, ze krawedz trojakta rownobocznego rowna sie wysokosci rombu

26 mar 19:59
ite: Co chcesz obracać? podstawę czy ostrosłup? Czy wyobrażasz sobie, jak wygląda ostrosłup i ten
przekrój?
26 mar 20:03
jaros: Jeżeli mój rysunek jak mówisz jest błędny to nie wiem jak wygląda

26 mar 20:06
ite: f123 ta informacja wynika z położenia wysokości ścian bocznych.
Przekroj zaznaczony na rysunku z 19:40 nie spełnia warunków zadania!
26 mar 20:07
jaros: @ite narysował byś mi poprawny, possszee chce zrozumieć to zadnie
26 mar 20:07
ite: jaros Czy wszystkie krawędzie ostrosłupa mają jednakowa długość?
Narysuj trójkąt stanowiący ścianę boczną i zaznacz na nim wysokość.
26 mar 20:09
ite: *krawędzie boczne ostrosłupa
26 mar 20:09
jaros:
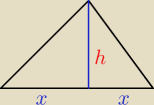
Coś takiego

?
26 mar 20:14
ite: narysuję, ale spróbuj najpierw sam wyobrazić sobie, że to nie jest ostrosłup prawidłowy (bo go
spłaszczyło)
26 mar 20:15
jaros: Dobrze, lecz wydaje mi się, ze spłaszczania figur jestem zielony jak szczypiorek na wiosnę
26 mar 20:19
ite:
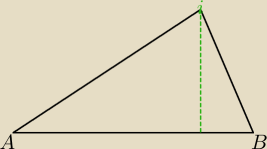
Krawędzie boczne ostrosłupa nie mają jednakowej długości. Dwie są równe i dłuższe, dwie
pozostałe tez równe i od nich krótsze.
Ściana boczna jej wysokość wyglądają tak jak na rysunku.
26 mar 20:19
ite: Za kwadrans zrobię model 3D, to będzie łatwiej zobaczyć.
26 mar 20:21
jaros: Lecz jak się to miewa w tym iż wysokość rombu jest postawą trójkąta przekroju? to wynika z
jakiego twierdzenia?
26 mar 20:28
jaros: bum ktoś pomoże?

26 mar 20:59
a7: mogę wkleić link do rozwiązania Mili? ale nie chcę zepsuć zabawy...
26 mar 21:01
26 mar 21:02
jaros: Ale przecież to nie to zadanie
26 mar 21:05
jaros: Aaaa na dole, dobra dziękuję
26 mar 21:05
jaros: Ale powie mi ktoś dlaczego tam jest trójkąt równoboczny?
26 mar 21:10
26 mar 21:10
ite: Bo tak jest w treści zadania, którą podałeś.
26 mar 21:11
a7: 22:56 w linku spodek wysokości ściany bocznej nie leży na środku podstawy, może o to Ci chodzi?
26 mar 21:12
Mila:
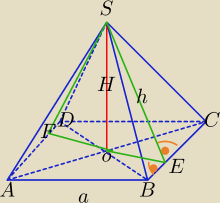
|EF|=8
26 mar 21:14
jaros: Ale piękny model

"Spodek wysokości ostrosłupa jest środkiem symetrii podstawy" ta informacja
nakierowuje nas na to, że wysokość w rombie jest też podstawą płaszczyzny, pytam dla
dopełnienia
26 mar 21:24
Mila:
Wysokość w rombie jest podstawą ( bokiem) szukanego przekroju.
26 mar 21:33

 ?
?
 ? nie mam bladego pojęcia o czym mi to
mówi xD
? nie mam bladego pojęcia o czym mi to
mówi xD


 Coś takiego
Coś takiego ?
?
 Krawędzie boczne ostrosłupa nie mają jednakowej długości. Dwie są równe i dłuższe, dwie
pozostałe tez równe i od nich krótsze.
Ściana boczna jej wysokość wyglądają tak jak na rysunku.
Krawędzie boczne ostrosłupa nie mają jednakowej długości. Dwie są równe i dłuższe, dwie
pozostałe tez równe i od nich krótsze.
Ściana boczna jej wysokość wyglądają tak jak na rysunku.

 |EF|=8
|EF|=8
 "Spodek wysokości ostrosłupa jest środkiem symetrii podstawy" ta informacja
nakierowuje nas na to, że wysokość w rombie jest też podstawą płaszczyzny, pytam dla
dopełnienia
"Spodek wysokości ostrosłupa jest środkiem symetrii podstawy" ta informacja
nakierowuje nas na to, że wysokość w rombie jest też podstawą płaszczyzny, pytam dla
dopełnienia