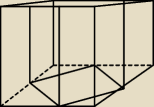
nietypowe zad jaros: Ile jest równa objętość wielościanu, którego wierzchołkami są środki krawędzi dowolnego czworościanu o objętości V?

	1		1
Przepraszam za rysunekXD ale mógłby mi ktos powiedziec dlaczego odp		V a nie		V
	2		8

skoro objętość to abc a środki to równoważnie połowki

a7: czworościan to nie prostopadłościan

salamandra: czworościan to ostrosłup a nie graniastosłup, to po pierwsze

a7: https://matematykaszkolna.pl/forum/274363.html

a7: https://forum.zadania.info/viewtopic.php?t=73026

jaros:

	1
4*		V bo mamy 3 naroża na dole i jedno u góry?
	8

a7: tak

a7:

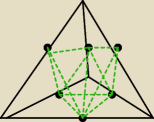
Mila: V_ABCS=V Odcinasz 4 naroża (jak u a7)

	1
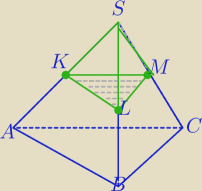
Ostrosłup KLMS jest podobny do ostrosłupa ABCS w skali k=
	2

Stosunek objętości brył podobny jest równy sześcianowi skali podobieństwa.

VKLMS		1
	=(		)3
VABCS		2

	1
VKLMS=		*V
	8

	1		1
Vb=V−4*		V=		*V− objętość bryły, która pozostaje po odcięciu 4 naroży.
	8		2