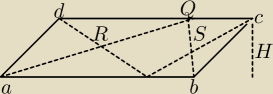
 Dany jest równoległobok ABCD. Na bokach AB i CD obrano odpowiednio punkty P i Q. odcinki AQ i
Dp przecinają się w punkcie R, a odcinki BQ i CP − w punkcie S. Wykaż, że suma pól trójkątów
APR i PBS jest równa sumie pól trójkątów DQR i QCS
Powie mi ktoś od czego zacząć?
Dany jest równoległobok ABCD. Na bokach AB i CD obrano odpowiednio punkty P i Q. odcinki AQ i
Dp przecinają się w punkcie R, a odcinki BQ i CP − w punkcie S. Wykaż, że suma pól trójkątów
APR i PBS jest równa sumie pól trójkątów DQR i QCS
Powie mi ktoś od czego zacząć?
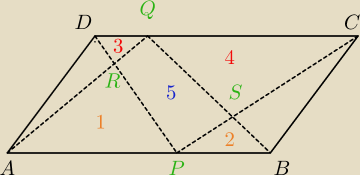 Zauważ, że PΔAQB = P{ΔCPD) (taka sama podstawa, taka sama wysokość
Lewa = PΔAQB = P1 + P2 + P5
Prawa = P{ΔCPD) = P3 + P4 + P5
Wniosek
Zauważ, że PΔAQB = P{ΔCPD) (taka sama podstawa, taka sama wysokość
Lewa = PΔAQB = P1 + P2 + P5
Prawa = P{ΔCPD) = P3 + P4 + P5
Wniosek 
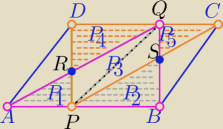 P− pole równoległoboku ABCD
P− pole równoległoboku ABCD
| 1 | ||
PΔABQ= | P=PΔDCP1 | |
| 2 |
| 1 | ||
P1+P2+P3= | P | |
| 2 |
| 1 | ||
P4+P5+P3= | P | |
| 2 |