uzasadnij trudne: Dany jest rownoleglobok ABCD. Na bokach AB i CD obrano odpowiednio punkty P i Q. Odcinki AQ i DP przecinają sie w punkcie R, a odcinki BQ i CP w punkcie S. Wykaz, ze suma pól trójkątów APR i PBS jest równa sumie pól trójkątów DQR i QCS.

trudne: Pomoże jeszcze ktoś o tej porze ?

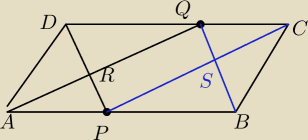
Qulka: Pole ABQ = Pole DCP bo ta sama wysokość równoległoboku i te same podstawy obustronnie odejmuję pole czworokąta PSQR Pole ABQ − PSQR= Pole DCP −PSQR zostają pola szukanych trójkątów (APR +PBS) = (CSQ + QRD)

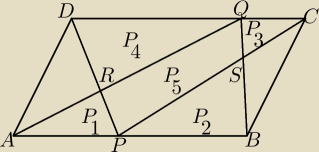
Bogdan: Łatwe: P₁, ..., P₅ pola powierzchni P_ABQ = P₁ + P₂ + P₅ P_CDP = P₃ +P₄ + P₅ P_ABQ = P_CDP ⇒ P₁ + P₂ + P₅ = P₃ +P₄ + P₅ ⇒ ...

Qulka: ale nam równo wyszło

Bogdan: