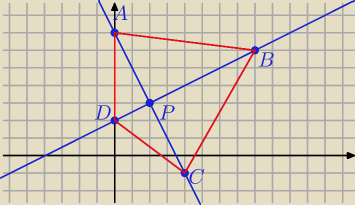
Proszę o szybką pomoc NiedzielnyMaturzysta: Przekątne AC i BD deltoidu ABCD mają taką samą długość i zawierają się odpowiednio w prostych k:2ax+y−7=0 oraz l:x−(a+1)y+4=0. Proste k i l przecinają się w takim punkcie P, że IDPI:IPBI = 1:3. Wiedząc, że punkt D należy do osi OY, oblicz wspołrzędne wierzchołków A, B, C, D tego deltoidu.

janek191: k : 2ax + y − 7 = 0 ⇒ y = −2ax + 7

	1		4
l : x − (a + 1) y + 4 = 0 ⇒ (a + 1) y = x + 4 ⇒ y =		x +
	a+1		a + 1

Proste są prostopadłe, więc

	1
−2a *		= −1
	a + 1

to a = 1 y = −2 x + 7

	1
y =		x + 2
	2

−2 x + 7 = 0,5 x + 2 −4 x + 14 = x + 4 5x = 10 x = 2 y = 3 P = ( 2,3) Dokończ

NiedzielnyMaturzysta: Nie wiem czy to przez zmęczenie czy przez głupotę ale nie jestem w stanie tego dokończyć, nie mam po prostu pomysłu na wyliczenie reszty

a7: oblicz długość |DP| oblicz długość |DB| =4|DP| podziel na dwa i wyznacz wierzchołki A i C z wzoru na długość odcinka

NiedzielnyMaturzysta: Ale jak mam obliczyć długość IDPI?

a7: D=(0,2) P=(2,3) |DP|=√5 |DB|=4√5 |AP|=|PC|=2√5 A=(x_A, −2x_a+7) C=(x_c,−2x_c+7) √(2−x)²)+(3+2x−7)²=2√5 x=0 i y=7 lub x=5 i y−3 analogicznie wyznaczamy punkt B DB=4√5 4√5=√x²+(1/2x+2−2)² x_B=8 y_B=6 lub x=−8 y_B=−2

a7: tu jest wzór https://matematykaszkolna.pl/strona/1248.html

a7: x=−8 y=−2 odrzucamy

NiedzielnyMaturzysta: Jezus dziękuje zapomniałem o tym że D leży na osi OY i nie wiedziałem skąd mam go wziąć żeby policzyć hyh 😓😓