planimetria
salamandra:
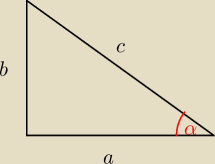
Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny. Oblicz tangens jednego z kątów
ostrych trójkąta.
(a,b,c)− ciąg arytmetyczny
lub (a,a+r,a+2r)
a
2+b
2=c
2
Nie wiem jak to połączyć ze sobą
22 mar 13:45
Jerzy:
Najwygodniej oznacz boki: x − 1 , x , x + 1
22 mar 13:48
salamandra: a nie jest to od razu de facto założenie, że r=1?
22 mar 13:49
Jerzy:
Upss .... oczywiście zamiast 1 miało być r
22 mar 13:49
salamandra: chociaż w tym wypadku chyba nie ma to znaczenia, bo każdy ten bok zwiększamy o tę stałą?
22 mar 13:50
salamandra: ok
22 mar 13:50
salamandra:
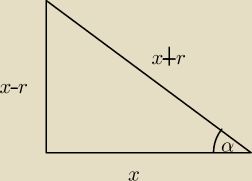
hm, no to mamy:
x
2+(x−r)
2=(x+r)
2
x
2+x
2−2xr+r
2=x
2+2xr+r
2
2x
2−2xr+r
2=x
2+2xr+r
2
x
2−4xr=0
x(x−4r)=0
x=0 v x=4r
x=0 ∉ D
x=4r
tędy droga?
22 mar 13:55
Jerzy:
22 mar 14:10
Eta:
Trójkąt ,którego długości boków tworzą ciąg arytmetyczny ,to trójkąt egipski
3,4,5 , 6,8,10,.....
tgα=3/4 lub 4/3
22 mar 14:12
Jerzy:
Słyszałeś o „złotym trójkącie” ?
22 mar 14:12
salamandra: Dzięki
22 mar 14:14
salamandra: Nie, o Pitagorejskim tylko, chyba ze to to samo
22 mar 14:14
22 mar 14:15
22 mar 14:19
salamandra: Czyli egipski to tylko 3,4,5?
22 mar 14:19
salamandra: Eciu, jestem "nocnym markiem" i takiego trudnego zadania, to wolę się wieczorem podjąć
(ale
pamiętam
22 mar 14:20
an: Różne drogi prowadzą do Rzymu. Zacząłeś dobrze dalej :
2b −a=c
c
2=(2b −a)
2=a
2+b
2
4b
2 −4ab+a
2=a
2+b
2
3b
2−4ab=0
22 mar 15:49
salamandra:
22 mar 16:05
Eta:
Tylko nie do Rzymu! ......
22 mar 16:40
https://matematykaszkolna.pl/forum/398599.html