geometria analityczna
salamandra: https://matematykaszkolna.pl/strona/4905.html
Czemu w tym zadaniu nie mogę zastosować wzoru na odległość prostej od punktu, tj. prostej na
której leży środek od np. punktu B i dlaczego to nie wyznacza mi dlugości promienia? Bo ten
kąt prosty w przypadku promienia jest na "wysokości" punktu, a nie na prostej na której leży
środek? (nie wiem jak to ugryźć w słowa, nie bijcie
)
22 mar 00:39
22 mar 00:42
salamandra: Już to widziałem
, ale nie rozumiem dlaczego moje postępowanie jest niepoprawne
22 mar 00:43
Eta:
Odległość B od tej prostej nie jest równa r
22 mar 00:48
salamandra:
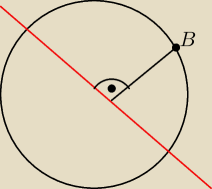
Dlatego, że w przypadku tego wzoru, tak jak napisałem, ten kąt prosty jest w tę stronę, a nie w
drugą?
22 mar 00:49
Eta:
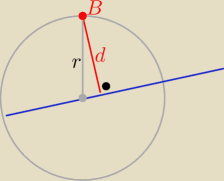
22 mar 00:51
salamandra: dzięki za potwierdzenie
22 mar 00:54
Eta:
Jak jeszcze przedłużą wolne i przełożą termin matur
to
roztrzaskasz maturę na 300%
22 mar 00:58
salamandra: bez przesady
>60% bym się już cieszył
22 mar 01:10
Eta:
Zadanko na dobranoc
1/ Na okręgu o promieniu "r" opisujemy wielokąty foremne
Podaj wzór ciągu jaki tworzą boki tych wielokątów i wykaż,że ten ciąg jest malejący
Powodzenia
22 mar 01:19
salamandra: Jutro (dziś) spróbuję, teraz już nie dam rady.. dopiero skończyłem maturkę z 2017 robić.., ale
dziękuję za zadanie
22 mar 01:26
Eta:
Ok ....Miłych snów
22 mar 01:28
salamandra: Dobranoc
22 mar 01:29
Eta:
Zadanie dalej ........ czeka na rozwiązanie
22 mar 22:01
salamandra: Nie wiem jak ruszyć, jest zbyt ogólne
nie wiadomo nawet jakie wielokąty
22 mar 22:04
Eta:
Wielokąty foremne !
22 mar 22:05
salamandra: no tak, ale niepowiedziane czy ma to być trójkąt, czy kwadrat, czy coś innego fajnego
22 mar 22:09
Saizou :
Spróbuj uzależnić długość boku od r i ewentualnie od jakiegoś kąta
22 mar 22:09
Saizou :
Chodzi o ciąg jaki tworzą kolejne boki wielokątów
bok trójkąta > bok kwadratu > bok pięciokąta > ...
22 mar 22:10
Patryk: Oby przełożyli matury bo inaczej cienko to widze w moim przypadku
22 mar 22:12
salamandra: Czemu? Zauważyłem, że robisz postępy
22 mar 22:12
Patryk: Postępy robię od września
chodzi głównie o czas, przez ruchy mojej matematyczki jestem do
tyłu z materiałem
22 mar 22:14
salamandra: nie martw się tą pochodną!
22 mar 22:15
salamandra: Dobra, ale nie wiem w jaki sposób mam to uzależnić, muszę najpierw założyć jaki wielokąt
rozważam?
22 mar 22:15
Patryk: nie tylko pochodna
a wypadało by kilka dni wygospodarować na lektury
22 mar 22:16
salamandra: ach.. nie przypominaj, nie znam ani jednej
przyznaję się bez bicia
22 mar 22:17
Eta:
22 mar 22:18
Saizou :
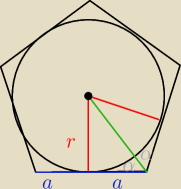
Suma kątów w n−kącie wynosi S
n=(n−2)/180°
Kąty wewnętrzne w n−kącie foremnym są równe, zatem
kombinuj dalej
22 mar 22:23
22 mar 22:25
salamandra: pierwsza linijka na pewno dobrze?
22 mar 22:26
Saizou : tam mnożenie
S
n =(n−2)•180°
22 mar 22:26
Eta:
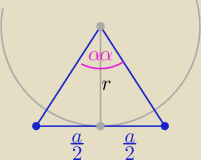
n ≥3 −− ilość boków
2α=360
o/n ⇒ α= 180
o/n
a=2r*tg(180
o/n)
a
1=.....
a
n=....
22 mar 22:33
salamandra:
coś w ten deseń trzeba kombinować?
22 mar 22:33
Eta:
Żyjesz?
22 mar 22:36
salamandra: No zadałem pytanie w tym samym czasie co odpowiedziałaś
22 mar 22:37
salamandra: Dlaczego u Ciebie 2α się różni w stosunku do tego co napisał Saizou?
22 mar 22:40
Eta:
Ja przez 2α zaznaczyłam kąt środkowy
22 mar 22:41
Saizou :
Eta bierze inny kąt .
22 mar 22:42
salamandra: Aha!
22:33, dobrze próbowałem, bo nie chce kontynuować w błędzie w razie co
22 mar 22:44
salamandra: Hm?
22 mar 23:26
Saizou :
| | r | |
Jak robisz z mojego rysunku to tgα= |
| |
| | a | |
22 mar 23:27
salamandra: aa, zapomniałem, że ty (zwykle) zaznaczasz 2a jako bok
22 mar 23:28
Saizou :
to masz też uproszczenie
| | (n−2)180 | | 90n−180 | | 180 | |
α= |
| = |
| =90− |
| |
| | 2n | | n | | n | |
| | 180 | | 180 | |
tgα=tg(90− |
| )=tg( |
| ) |
| | n | | n | |
22 mar 23:31
Saizou : Po prostu jak widzę trójką równoramienny, to lepiej nazwać podstawę wielokrotnością liczby 2
22 mar 23:32
22 mar 23:35
salamandra: no ok, czyli w tym momencie
a*tgα=r
22 mar 23:39
22 mar 23:39
Saizou :
możesz zostać przy postać
no bo to bez różnicy czy będziemy rozważać cału bok czy jego połowę
22 mar 23:44
salamandra: i teraz chodzi o ciąg, w sensie jak będzie wpisywany wielokąt z coraz większą boków wpisywany,
to jak będzie sie zmieniała jego długość?
22 mar 23:47
Saizou : tak, musisz zbadać monotoniczność ciągu
Lepiej napisać komentarz słowny
albo: złożenie funkcji rosnącej i malejącej daje funkcję malejącą
22 mar 23:50
22 mar 23:53
salamandra: Nie mogę skomentować po prostu, że dla coraz większych "n" wartość tg będzie mniejsza więc w
rezultacie ten ciąg będzie malejący?
22 mar 23:55
Saizou :
Można
22 mar 23:57
salamandra: to w końcu w mianowniku n, czy n+2?
22 mar 23:57
Saizou :
Eta właśnie, dlaczego n+2? Chyba już późno
22 mar 23:59
salamandra: A co w przypadku tg90? przecież nie istnieje?, dla n=2, będzie tg90?
23 mar 00:00
salamandra: a, nieważne, przecież wielokąt nie ma dwóch boków
23 mar 00:00
Saizou : dla n = 2 nie istnieje wielokąt
23 mar 00:01
salamandra: Dzięki za pomoc!
23 mar 00:05
Eta:
Jeżeli a
n −−− ciąg ,to istnieją wszystkie wyrazy a
1,a
2,a
3,...
zatem
poprzednio nie dopisałam 2r ( dwójką mi zżarło
23 mar 00:17
Saizou : @Eta nie zgodzę się z tobą, równie dobrze możemy zdefiniować ten ciąg od n ≥3
23 mar 00:22
Eta:
Na jedno wychodzi
Ja definiuję dla n≥1 a Ty dla n≥3
23 mar 00:23
Saizou : Zresztą na monotoniczność i tak to nie wpływa
23 mar 00:26
Eta:
23 mar 00:27