zad opymalizacyjne jaros: Dany jest punkt A = (a, b) leżący na paraboli f (x) = x2 dla 3D którego 1 ≤ a ≤ 2. Punkt B jest punktem przecięcia stycznej do wykresu funkcji y = f(x) w punkcie A z osią OX, 2C = (2, 0) oraz punkt D jest punktem przecięcia prostej x = 2 ze styczną (zobacz rysunek). Dla jakiego punktu A 1A pole trójkąt BCD jest największe, a dla jakiego A pole to jest najmniejsze?

wredulus_pospolitus: pokaż rysunek ... albo go zrób tutaj

wredulus_pospolitus: wyznacz ogólną postać stycznej do wykresu f(x) = x² w punkcie A(a, b)

jaros: https://imgur.com/I3wrBFo nie wiem jak to tutaj narysować

wredulus_pospolitus: Tak jak napisałem Zał. a ∊ <1,2> Krok 1: wyznacz ogólna postać równania stycznej do wykresu f(x) = x w punkcie P(a, a²) Krok 2: wyznacz punkt przecięcia się tejże prostej z osią OX Krok 3: wyznacz punkt przecięcia się tejże prostej z prostą x = 2 Krok 4: wyznacz długości boków trójkąta: BC i CD Krok 5: wyznacz funkcję pola tego trójkąta prostokątnego Krok 6: wyznacz minimum tejże funkcji pola

wredulus_pospolitus: Tutaj: https://matematykaszkolna.pl/forum/398151.html było robione bardzo podobne zadanie. Robisz ANALOGICZNIE.

wredulus_pospolitus: Możesz też 'szturchnąć' salamandrę ... może maturzysta maturzyście to przystępniej wytłumaczy

salamandra: Później spróbuję to rozwiązać, jeśli mi powiesz co to 3D oraz 2C i „A 1A”

salamandra: hm?

jaros: Dany jest punkt A = (a, b) leżący na paraboli f (x) = x² dla którego 1 ≤ a ≤ 2. Punkt B jest punktem przecięcia stycznej do wykresu funkcji y = f(x) w punkcie A z osią OX, C = (2, 0) oraz punkt D jest punktem przecięcia prostej x = 2 ze styczną (zobacz rysunek). Dla jakiego punktu A pole trójkąt BCD jest największe, a dla jakiego A pole to jest najmniejsze?

jaros: tutaj poprawiona wersja, sorki że tak późno ale musiałem coś załatwić... biorę się za rozwiązanie hmmm...

jaros: P(a,a²) a=2x₀ b=−x₀²

	x02
Bok BC =
	I2x0I

Bok DC = x₀²

	(x02)2
Pole =		? ktoś sprawdzi czy to dobrze rozpisałem
	4x0

jaros: pole jest przed różniczkowaniem

salamandra: co to jest P?

jaros: P=A tak oznaczyłem jak wredulus_pospolitus

Bleee: Jaki jest wzór stycznej?

Bleee: Długości boków nie zgadzają się chociażby dla A(1, 1)

salamandra: Spróbujmy razem: A=(a,b) a∊<1;2> A=(a,a²) f'(x)=2x f'(a)=2ax równanie stycznej: y=2ax(x−a)+ax²

Bleee: Salamandra − f'(a) = 2a a nie 2ax

Bleee: Wyraz wolny jeszcze gorzej wyliczony. To co napisałeś to wykres paraboli jakiejś a nie prostej

Leszek: Styczna to ma rownanie liniowe ! a nie jest funkcja kwadratowa !

salamandra: pier***ca dostaje od tych literek, a wahałem się czy napisać 2a czy 2ax f'(x)=2x f'(a)=2a równanie stycznej: y=2a(x−a)+a², teraz git?

Bleee: Oooo... Teraz jest git

jaros: Bleee a mógłbyś mi powiedzieć co i jak zrobić by policzyć dobrze?

salamandra: Cicho, on będzie sprawdzał, robimy we dwóch

Bleee: Zostawię to salamandrze... Niech chłop przećwiczy Ja sprawdzę zapiski

jaros: salamandra a powiesz mi czemu liczymy f'(a)? tzn od tego punktu tak? a co zróżniczkowałeś żeby otrzymać 2a?

salamandra: Będę po kawałku pisał, zeby nie robić z błędem dalej w razie co. miejsce zerowe stycznej wyznaczy nam współrzędną "x" punktu B. y=2ax−4a²+a² b=−4a²+a²

	−(−4a2+a2)		4a2−a2
miejsce zerowe:		=		?
	2a		2a

salamandra: pochodna funkcji f(x)=x² to f'(x)=2x ze wzoru na styczną musimy wyznaczyć f'(x0) (w naszym przypadku f'(a), więc f'(a)=2a

jaros: aaa czyli moje f'(x₀) to tutaj f'(a) ?

salamandra: nie widzę u Ciebie f'(x0) nigdzie

wredulus_pospolitus: jarus odnosi się do wzoru z teorii ... gdzie występuje P(x_o , f(x_o) )

wredulus_pospolitus: Źle wyliczone miejsce zerowe ... a raczej −−− źle przekształcony wzór stycznej y = 2ax − a²

	a
0 = 2ax − a2 −−−> x =
	2

jaros: b = y0 − ax0 b = a² − 2a*a² = −a²?

wredulus_pospolitus: poprawić ... wyznaczyć drugi punkt przecięcia (wierzchołek trójkąta) i wyznaczyć długości boków

wredulus_pospolitus: jaros −−− co Ty teraz policzyłeś −ax_o = −2a*a² cokolwiek to jest −−− to jest źle

jaros: a tak racja

salamandra: Nie wiem skąd ja 4a² wzialem xd

jaros: miesza mi sie zapis salamandry z moim dlatego te błędy, rozumiem już gdzie jest błąd lecz czy nie powinna być jeszcze nałożona wartość bezwzględna na a?

jaros: No chyba ze założenie to wyklucza

jaros: ej ale tak wsm to ja to chyba w miarę dobrze mam

wredulus_pospolitus: jaros −−− dlaczego? a ∊ <1;2> −−−− podane w treści zadania ... więc a > 0 ... moduł całkowicie zbyteczny

salamandra: Za 5 minut będę kontynuowal

wredulus_pospolitus: Ale że co masz dobrze To co napisałeś o 21:49 ni jak się ma do 'dobrze'

wredulus_pospolitus: No i Miluś zepsuła zabawę maturzystom .... wstydziłaby się niewiasta

jaros:

	x0
To jak różniczkować teraz to pole? Bo ile wyonszą boki BC =		a DC = x02?
	2

salamandra: Nie No Mila.. foch

Mila:

wredulus_pospolitus: Nie ... |BC| ani |DC| ABSOLUTNIE tyle nie wynoszą

wredulus_pospolitus: (wpis tyczy się jaros'a)

salamandra: Mimo to, nie zaglądam i spróbuje sam

jaros: Mila a wytłumaczyła byś mi punkt 4? d= nie wiem skąd się wzięły parametry tego punktu

jaros: A rozumiem podstawione do równania stycznej przechodzącej przez punkt a jeszcze gdybyś mi mogła powiedzieć to z jakiej własności jest punkt 6?

Mila: Za chwilę, rysuję

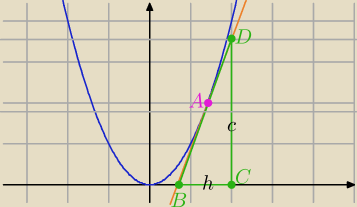
Mila: 1) Na rysunku punkt D powinien leżeć na stycznej i prostej x=2 , jak rysowałam, to nie wiedziałam, jakie ma współrzędne, a potem nie poprawiłam. D=(2,d) y=2ax−a² − r. stycznej d=2a*2−a²=4a−a² 2) Pole Δ prostokątnego :

	1		1		a
PBCD=		*h*c=		*(2−		)*(4a−a2)
	2		2		2

jaros: Przepraszam chodziło o punkt 5, z jakiej własności dlugosc boku = współrzędnej d?

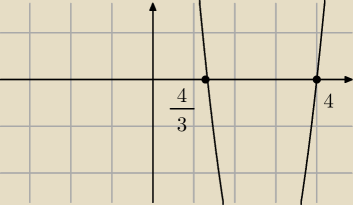
salamandra: Kontynuuję: równanie stycznej: y=2a(x−a)+a² y=2ax−2a²+a²= 2ax−a²

	−b
miejsce zerowe:
	a

	a2		a
miejsce zerowe:		=
	2a		2

	a
B=(		, 0)
	2

C=(2,0)

	a		4−a
|BC|=2−		=
	2		2

D=(2,2ax−a²)= (2,4a−a²) |CD|=4a−a²

	1		1		4−a
P=		*|BC|*|CD|=		*		*(4a−a2) =
	2		2		2

	4−a		(4−a)4a		(4−a)a2
		*(4a−a2)=		−		=
	4		4		4

	16a−4a2		4a2−a3		a3−8a2+16a
=		−		=
	4		4		4

f(a)=a³−8a²+16a f'(a)=3a²−16a+16 f'(a)=0 ⇔3a²−16a+16=0 Δ=256−192=64 √Δ=8

	16−8		8		4
a1=		=		=
	6		6		3

	16+8
a2=		=4
	6

	4
maks. dla a=
	3

min dla a=4 Dobrze?

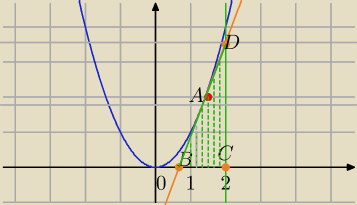
Mila: Właściwa treść zadania: Dany jest punkt A=(a,b) leżący na paraboli f(x)=x2 dla którego 1≤a≤2. Punkt B jest punktem przecięcia stycznej do wykresu funkcji y=f(x) w punkcie A z osią OX, C=(2,0) oraz D jest punktem przecięcia prostej x=2 ze styczną. Dla jakiego A pole trójkąta BCD jest największe, a dla jakiego A pole to jest najmniejsze? 1) f(x)=x² A=(a,a²) f'(x)=2x f'(a)=2a 2) Styczna: y=f'(a) (x−a)+f(a) y=2a*(x−a)+a² y=2ax−a² 3) Punkt B− jest punktem przecięcia stycznej z osia OX⇔y=0 2ax−a²=0 2ax=a² a≠0 2x=a

	a
x=
	2

	a
B=(		,0)
	2

4) D=(2,d) d=2a*2−a2 d=4a−a2 D=(2,4a−a2) 5) |CD|=|4a−a²| i 1≤a≤2⇔ |CD|=4a−a² h− odległość punktu B od prostej x=2

	a
h=2−
	2

6) ΔBCD− trójkąt prostokątny

	1
PΔBCD=		*|BC|*|CD|
	2

	1		a		1
P(a)=		*(2−		)*(4a−a2)=U{1}[2}*(		a3−4a2+8a)
	2		2		2

	1		3
P'(a)=		*(		a2−8a+8) i 1≤a≤2
	2		2

Teraz licz i wyznaczaj a dla pola największego i najmniejszego. Może teraz nie ma pomyłek w redagowaniu. Jeśli są to poprawiajcie.

salamandra: Stop zapomniałem o warunku a∊<1;2>

salamandra: Maks sie nie zmieni, ale min dla a=2 bodajże

Mila: a=4∉D to musisz poprawić

jaros: Wszystko dobrze ale powiedzcie mi z jakiej własności |CD|=4a−a2 prooosze

salamandra: no odległość od C do D

salamandra: skoro C=(2,0), D=(2,4a−a²) to odleglosc miedzy nimi to roznica między wspolrzednymi "y", bo x jest ten sam

jaros: Ok Dziękuje ślicznie

jaros: Wszystko jest piknie, 65 odpowiedzi ale natrzaskane hahah ale zadanie wytłumaczone dokładnie ^^

salamandra: Moje dość regularnie przekraczają 100