optymalizacja
salamandra:
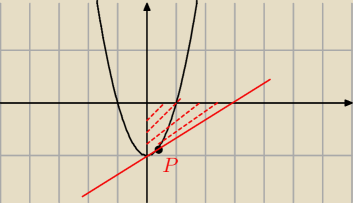
W jakim punkcie paraboli o równaniu y=x
2−1 należy poprowadzić styczną, aby trójkąt ograniczony
tą styczną i osiami układu współrzędnych miał najmniejsze pole?
y=x
2−1
P=(x,x
2−1)
f'(x)=2x
Jakaś podpowiedź?
15 mar 22:50
Patryk: Tak zapytam z ciekawości bo i tak pochodnych nie zacząłem, pochodne prostsze od
prawdopodobieństwa i kombinatoryki?

15 mar 22:57
salamandra: Zależy od osoby− dla mnie pochodne to była jedna z najprostszych rzeczy podczas edukacji w
technikum
15 mar 22:57
Patryk: A dla mnie kombinatoryka najtrudniejszą rzeczą w technikum

15 mar 22:58
Patryk: A jak z optymalizacją, dajesz rade?
15 mar 23:00
salamandra: Bywa ciężko, ale w większości schemat jest ten sam. Stereometria+optymalizacja to trochę
kombinowania jest
15 mar 23:01
Patryk: A te pochodne w tych zadaniach to wykorzystuje się tylko po to żeby wyznaczać te wartości min
albo max?
15 mar 23:02
salamandra: zazwyczaj tak, albo jak w tym przypadku− styczna do wykresu funkcji, generalnie do badania
monotoniczności funkcji
15 mar 23:03
wredulus_pospolitus:
krok 1:
Punkt styczności (to masz)
krok 2:
wyznaczenie równania stycznej w punkcie P (f(x))
krok 3:
f(0) = a
f(x) = 0 −−−> b = ...

krok 4:
Pole(x) = a*b = ....
krok 5:
Pole'(x) = ...
15 mar 23:18
salamandra: No właśnie, jak wyznaczyć równanie tej stycznej jeśli nie znam punktu P?
y=ax+b
a=2x
x
2−1=2x*x+b
x
2−1=2x
2+b
b=−x
2−1
y=2x*x−x
2−1 = x
2−1, czyli wróciłem de facto do paraboli

15 mar 23:20
wredulus_pospolitus:
równanie stycznej do wykresu g(x) = x2−1 w punkcie P(xo, xo2 − 1)
y − (xo2 −1) = 2xo(x − xo)
y = 2xo*x + (xo2 − xo − 1)
f(x) = 2xo*x + (xo2 − xo − 1) <−−− równanie stycznej (dla określonego punktu P,
czyli dla określonego xo)
15 mar 23:23
wredulus_pospolitus:
oczywiście źle podałem wyraz wolny na końcu ... to już sobie to popraw
15 mar 23:26
salamandra: Gdzieś się pomyliłem? Co jakbyś się trzymał wersji y=ax+b?
15 mar 23:27
salamandra: a, no właśnie, wiedziałem, że coś mi nie gra

ale dlaczego piszesz x
0, a nie po prostu x?
15 mar 23:28
salamandra: Z tego wynika jakby x0 było czymś innym niż x, a przecież leży na paraboli również.
15 mar 23:28
wredulus_pospolitus:
bo punkt P ma współrzędne (xo, xo2 − 1)
Albo jak wolisz:
krok 1: wybieramy punkt P (czyli wyznaczamy x = xo)
krok 2: Dla współrzędnych tego konkretnego punktu (czyli dla konkretnej wartości xo)
wyznaczamy styczną
15 mar 23:30
wredulus_pospolitus:
y = 2xo*x − (x2o+1) <−−− tak wygląda równanie stycznej
15 mar 23:31
salamandra: Aha, a pisząc gołe x, to tak jakby operuję dalej zmienną?
15 mar 23:33
wredulus_pospolitus:
tak
'x' −−− zmienna
'y' −−− zmienna
x
o −−− konkretna (bliżej nie określona − ale konkretna

) wartość zmiennej 'x'
15 mar 23:34
salamandra: Chociaż w sumie nadal nie rozumiem, bo np. Dajmy na to jakieś zadanie z okręgiem i tam często
stosujemy np. A(x, x2−1) i dlaczego tam już nie piszemy to x0?
15 mar 23:41
wredulus_pospolitus:
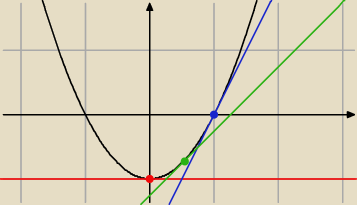
żeby Ci się nie 'pojebało' ze zmienną 'x' występującą w równaniu prostej
P(w,w
2−1)
styczna ma równanie y = 2w*x − (w
2 + 1)
weźmy, punkt P(0,−1)
y = 2*0*x − (0 + 1) −−−> y = −1 zgadza się
weźmy punkt P(1, 0)
y = 2*1*x − (1 + 1) −−−−> y = 2x − 2 także się zgadza
weźmy punkt P(1/2 , −3/4)
y = x − 5/4
15 mar 23:45
wredulus_pospolitus:
y i x są to zmienne reprezentujące współrzędne KAŻDEGO punktu na konkretnej prostej
xo (czy tam w) reprezentuje KTÓRĄ z tych stycznych bierzesz pod uwagę w danej chwili
15 mar 23:46
salamandra: teraz jaśniej, dobra kombinuję dalej

15 mar 23:47
salamandra:
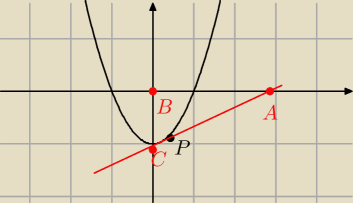
B=(0,0)
C=f(0)=w
2−1
A=(w,0)
|AB|=w
|BC|=w
2−1
f(x)=w
3−w
f'(x)=3w
2−1
3w
2−1=0
3w
2=1
15 mar 23:57
salamandra: f(w) oczywiście
16 mar 00:00
wredulus_pospolitus:
NIE

czemu |AB| = w

z jakiej racji

już nawet na Twoim rysunku z 23:57
P(w, w
2 − 1) ....
punkt A jest gdzieś w okolicach (3,0) ... więc co ... w = 3

nie ... w ≈ 1/3 (patrząc na
rysunek)
punkt C także źle wyznaczony ... f(0) = − (w
2 + 1)
16 mar 00:04
wredulus_pospolitus:
x = 0 −−−−> y = 0 −(w
2+1) −−−> |a| = w
2 + 1 (|a| −−− długość boku na osi OY)
| | w2+1 | | w2+1 | |
y = 0 −−−−> 0 = 2wx − w2 − 1 −−−> x = |
| −−−> |b| = |
| |
| | 2w | | 2w | |
(|b| −−− długość na boku OX)
sprawdzenie:
w = 1/2 (czyli styczna dla punktu P(1/2, −3/4)
y = x − 5/4
|a| = 1/4 + 1 = 5/4 oki
| | 1/4 + 1 | |
|b| = |
| = 5/4 oki |
| | 2*1/2 | |
w = 3/4 <−−− sprawdź sam
16 mar 00:04
salamandra: | | √3 | | −2 | | −√3 | | −2 | |
W odpowiedzi jest P= |
| , |
| ) lub P= |
| , |
| ). |
| | 3 | | 3 | | 3 | | 3 | |
Z tego co teraz napisałeś to kompletnie nic nie rozumiem.
Fakt, C źle wyznaczyłem, powinno być 2w*0−(w
2+1) = −w
2−1
16 mar 00:09
salamandra: I sam nie wiem skąd wziąłem że A=(w,0) XD
16 mar 00:10
wredulus_pospolitus:
No to popraw wyznaczenie:
|AB| i |BC|
16 mar 00:11
salamandra: "A" nie będzie miało współrzędnej po prostu miejsca zerowego tej stycznej?
16 mar 00:13
wredulus_pospolitus:
tak, dokładnie −−− miejsce zerowe ... ale to nie będzie to co napisałeś

16 mar 00:14
salamandra: y=2x*w−(w
2+1)
| | −b | | w2+1 | |
miejsce zerowe= |
| = |
| ? |
| | a | | 2w | |
|BC|=−w
2−1, bo punkt przecięcia z osią Y, to wyraz wolny?
16 mar 00:19
wredulus_pospolitus:
a czemu |BC| < 0

16 mar 00:20
wredulus_pospolitus:
poza tym −−− jest oki
16 mar 00:20
salamandra: no tak, bzdura, to jest odległość, czyli wartość bezwzględna z tego? ale jak wtedy doprowadzić
do w2+1?, wiem, że tyle będzie, ale nie wiem jak do tego dojść
|BC|=√(−x2−1)2
16 mar 00:21
wredulus_pospolitus:
√ −(w2+1)2 = |−(w2+1)| = w2 + 1
16 mar 00:22
salamandra: | | w2+1 | | 1 | | w4+w2+w2+1 | | 1 | | w4+2w2+1 | |
P= |
| *w2+1* |
| = |
| * |
| = |
| ? |
| | 2w | | 2 | | 2w | | 2 | | 4w | |
16 mar 00:27
Eta:
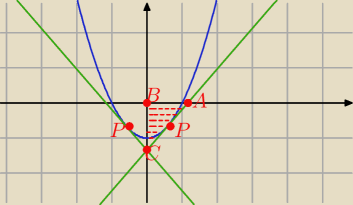
Pamiętaj ,że ze względu na parzystość funkcji
są dwa takie punkty P symetryczne względem osi OY
16 mar 00:31
salamandra: o matko... jeszcze coś...

16 mar 00:32
salamandra: rozwiązywałem źle− odpowiedź wyszła prawidłowa, robię dobrze i wynik mi wychodzi zły, to
dopiero paradoks...
16 mar 00:33
Eta:
Kontroluj rachunki ! (obliczenia) jak kasjer w Biedronce


16 mar 00:36
salamandra: Sprawdziłem to 00:27 z photomath, nigdzie się nie pomyliłem, nie wiem co jest grane
16 mar 00:36
jc: Najlepsza jest styczna w punkcie (1/√3, 1/3−1).
16 mar 00:47
Eta:
w≠0
| | 1 | |
P'(w)= U(1}{4}(3w2+2− |
| ) =0 |
| | w2 | |
3w
4+2w
2−1=0
i leć dalej .......................
| | √3 | | 2 | | √3 | | 2 | |
Odp: P( |
| , − |
| ) lub P(− |
| ,− |
| ) |
| | 3 | | 3 | | 3 | | 3 | |
16 mar 00:47
16 mar 00:48
salamandra: Skąd to P(w)?

?
16 mar 00:51
Eta:
P(w) −−− funkcja pola!
16 mar 00:53
Eta:
Punkt oznaczyłeś przez P
pole przez P i masz kolizję oznaczeń
16 mar 00:54
salamandra: Nie, akurat ta kolizja nic nie zmienia, bo mi z tej postaci funkcji w ogóle nie wychodzi to co
Tobie

16 mar 00:58
salamandra: Wiem ze funkcja pola, ale jak doszlas do tego zapisu, bo to troche inaczej niż u mnie
16 mar 00:59
Eta:
Po co oznaczasz współrzędne przez "w" ?
P(x,x
2−1)
|BC|=|−x
2−1|= x
2+1
to
.......................
16 mar 01:07
salamandra: To ja już dziś odpadam w takim razie, już się zagmatwalem kiedy to „w”, kiedy „x”, kompletna
przestrzeń kosmiczna dziś...
16 mar 01:09
wredulus_pospolitus:
| | w2+1 | | (w2+1)2 | |
P(w) = |
| *(w2+1)*0.5 = |
| |
| | 2w | | 4w | |
| | 4w(w2+1)*4w − 4(w2+1)2 | |
P'(w) = |
| |
| | 16w2 | |
| | √3 | |
licznik: (w2+1)[ 16w2 − 4(w2+1)] = (w2+1)[ 12w2 − 4 ] −−−−> w = ± |
| |
| | 3 | |
16 mar 01:15
jc: 0:19 y=2x*w−(w2+1)
Szukamy teraz przecięcia z osiami. Wynik wyrazi się przez w.
16 mar 01:17
salamandra: To może inaczej− co tu jest źle?
| | w2+1 | | 1 | | w4+w2+w2+1 | | 1 | | w4+2w2+1 | |
P(w)= |
| *(w2+1)* |
| = |
| * |
| = |
| |
| | 2w | | 2 | | 2w | | 2 | | 4w | |
| | (4w3+2)*4w−(w4+2w+1)*4 | | 16w4+8w−(4w4+8w+4) | | 12w4−4 | |
P'(w)= |
| = |
| = |
| ? |
| | 16w2 | | 16w2 | | 16w4 | |
16 mar 09:55
salamandra: na końcu w mianowniku oczywiście 16w2
16 mar 10:08
Jerzy:
| | (4w3 + 4w)*4w − (w4 + 2w2 +1)*4 | |
P'(w) = |
| |
| | 16w2 | |
16 mar 10:10
salamandra: nie wiem dlaczego zjadłem kwadrat przy 8w w nawiasie, dzieki Jerzy
16 mar 10:12
Jerzy:
W pierwszym nawiasie masz złą pochodną licznika.
16 mar 10:15
salamandra: Już wszystko widzę, dzięki raz jeszcze

ponad godzinę straciłem nad tym dziadostwem...
16 mar 10:17
salamandra:
mogę tutaj też badać tylko licznik, bo mianownik zawsze dodatni przez kwadrat?
jak tak, to
12w
4+8w
2−4=0
t=w
2 t≥0
12t
2+8t−4=0 / : 4
3t
2+2t−1=0
Δ=16
16 mar 10:27
Jerzy:
Tak.
16 mar 10:40
salamandra:
Czy wtedy wykres pochodnej będzie wyglądał tak?
16 mar 10:55
jc: Jak nie masz tego zupełnie dość, to spójrz na ten rachunek:
[(w
2+1)
2]' = 2(w
2+1) (w
2+1)' = 2(w
2+1)2w = 4w(w
2+1)
Teraz
| | (w2+1)2 | | [(w2+1)2]' w − (w2+1)2 w' | |
[ |
| ]' = |
| |
| | 4w | | 4w2 | |
| | 4w(w2+1)w − (w2+1)2 | |
= |
| |
| | 4w2 | |
Kiedy mamy zero?
4w
2(w
2+1)=(w
2+1)
2
4w
2=w
2+1
3w
2=1
−−−
Skąd się u Ciebie wzięło 16 w mianowniku?
16 mar 10:57
Jerzy:
Ściślej licznika pochodnej, ale to nas właśnie interesuje.
16 mar 10:59
salamandra: Jak wtedy dojść do tego o czym Eta powiedziała, że muszę pamiętać o symetrii? Bo z pochodnej
| | √3 | | −√3 | |
wynika, że dla |
| jest minimum, a dla |
| jest maksimum, a z tej symetrii |
| | 3 | | 3 | |
| | −√3 | |
wychodzi na to, że dla |
| jest również minimum. |
| | 3 | |
16 mar 11:02
salamandra: @jc,
| | w4+2w2+1 | |
no bo P(w)= |
| , więc pochodna ilorazu, to mianownik do kwadratu |
| | 4w | |
16 mar 11:04
Jerzy:
Zauważ ,że w tych punktach pochodna zmienia znak inaczej.
16 mar 11:05
salamandra: | | −√3 | |
Co masz na myśli Jerzy? czyli tu nie jest klasycznie, że od (−∞; |
| ) funkcja rośnie, |
| | 3 | |
| | −√3 | | −√3 | | √3 | |
więc w |
| osiąga maksimum, w przedziale ( |
| ; |
| ) maleje, więc w |
| | 3 | | 3 | | 3 | |
| | √3 | | √3 | |
|
| osiąga minimum i w przedziale ( |
| ; ∞) znów rośnie? |
| | 3 | | 3 | |
16 mar 11:08
Jerzy:
| | √3 | |
W punkcie x = − |
| pochodna zmienia znak z dodatniego na ujemny, czyli funkcja P(w) ma |
| | 3 | |
| | √3 | |
maksimum,natomiast w punkcie |
| zmienia znak z ujemnego na dodatni, czyli funkcja ma |
| | 3 | |
minimum.
Pamiętaj,że zerowanie sie pochodnej, to jedynie warunek konieczny istnienia ekstremum.
Warunkiem wystarczającym jest zmiana znaku pochodnej.
16 mar 11:13
salamandra: | | −√3 | |
No właśnie, w |
| osiąga maksimum, a według tej symetrii w tym punkcie owy trójkąt |
| | 3 | |
będzie miał NAJMNIEJSZE pole, tak jak napisała Eta 00:31
16 mar 11:15
jc: salamandra, 1/4 jest liczbą. 1/4 wyciągasz przed pochodną.
Oczywiście wynik będzie w każdym przypadku będzie taki sam.
16 mar 11:41
salamandra: W którym miejscu?
16 mar 11:42
jc: salamandra
(5f)' = 5 f', choć można liczyć tak:
(5f)' = 5' f + 5 f' = 5f'
podobnie
| | f | | f' | |
( |
| )' = |
| , choć można liczyć tak: |
| | 4 | | 4 | |
| | f | | f' 4 − f 4' | | f' 4 | | f' | |
( |
| )' = |
| = |
| = |
| |
| | 4 | | 42 | | 16 | | 4 | |
To, że stałą możemy wyciągnąć przed znak pochodnej jest bardziej podstawową
własnością niż wzory na pochodną iloczynu lub ilorazu.
16 mar 12:15
salamandra: Tak, tylko ja pytałem konkretnie o to, jak rozpoznać kiedy trzeba wziąć pod uwagę symetrię? Bo
| | −√3 | |
odpowiedzią w tym zadaniu będzie również |
| , a z pochodnej wychodzi na to, że tam |
| | 3 | |
jest maksimum
16 mar 12:17
Bleee:
Salamandra... Powiedz − gdzie trafiłeś na to zadanie?
16 mar 12:23
salamandra: Kiełbasa
16 mar 12:24
Bleee:
To Ci powiem − że z dnia na dzień coraz bardziej przekonany jestem do tego że Kiełbasa powinien
sobie darować robienie zbiorów zadań.
16 mar 12:26
salamandra: Za trudne?
16 mar 12:27
wredulus_pospolitus:
Nie jest trudne ... ale trzeba zwrócić uwagę na parę rzeczy.
16 mar 12:29
jc: Pole wyraża się przez iloczyn długości, a te są modułami.
| | (w2+1)2 | |
Funkcja jest parzysta: P(w)= |
| = P(−w). |
| | 4|p| | |
Bez modułu masz P(−w)=−P(w) i zamiast 2 minimów, masz minimum i maksimum.
16 mar 12:30
salamandra: No jest oznakowane na czerwono (dla rozszerzenia) i dodatkowo z gwiazdką
16 mar 12:31
Eta:
We wpisie 16 marca na wykresie)
00:31
Pierwsze pole trójkąta rozpatrujesz dla x>0
i ze względu na symetrię o osi OY
i po ptokach

16 mar 12:33
wredulus_pospolitus:
Zadanie od podstaw:
W jakim punkcie paraboli o równaniu y=x
2−1 należy poprowadzić styczną, aby trójkąt ograniczony
tą styczną i osiami układu współrzędnych miał najmniejsze pole?
1) Wyznaczamy wzór stycznej do wykresu f(x) w punkcie P o współrzędnych (w, w
2−1)
y − f(x
o) = f'(x
o)*(x − x
o)
y − (w
2−1) = 2w*(x − w)
y = 2w*x − (w
2 + 1)
2) wyznaczamy punkty przecięcia się stycznej z osiami OX i OY:
z OY −> 0 − (w
2+1) = a −> a = −(w
2+1) −> W punkcie (0, −(w
2+1) )
| | w2+1 | | w2+1 | |
z OX −> 0 = 2w*x − (w2+1) −−> x = |
| −> W punkcie ( |
| ,0) |
| | 2w | | 2w | |
3) Określamy długości boków przyprostokątnych w rozpatrywanym trójkącie
|BC| = w
2 + 1
4) Określamy wzór funkcji pola tegoż trójkąta:
| | |AB| * |BC| | | (w2+1)2 | |
Pole(w) = |
| = |
| |
| | 2 | | 4|w| | |
16 mar 12:36
Eta:
Po co się aż tak wysilać?

16 mar 12:37
wredulus_pospolitus:
I teraz jest istotna rzecz, której nie rozpatrywaliśmy wcześniej:
a) zauważamy, że funkcja Pole(w) jest funkcją parzystą i od tej pory liczymy tylko dla w>0 i
później odbijamy symetrycznie
b) liczymy dla w ∊ R/{0} rozdzielając funkcję Pole(w) na dwa przypadki (|w| = w oraz |w| = −w
<−−− w celu policzenia pochodnej)
16 mar 12:39
salamandra: No na to to bym nie wpadł.... niech już zapomnę o tym zadaniu....
Głupio mi się przyznać, ale nadal mam zagwostkę największą z tym, czemu punktu P nie można
określić poprzez (x,x2−1) skoro leży on na paraboli...
16 mar 12:39
Eta:
bo dla x>0 y=x
2−1 i dla x<0 też y=x
2−1
wniosek mamy dwa takie punkty
jasne?

16 mar 12:41
wredulus_pospolitus:
I to jest moment, na którym (moim zdaniem) maturzyście się wyłożą w tym zadaniu (bo nie ćwiczy
się tego na zajęciach).
16 mar 12:41
Eta:

16 mar 12:42
wredulus_pospolitus:
Salamandra ... odnośnie stycznej i współrzędnych punktu P.
Wzór ogólny na styczną do wykresu w punkcie P(x
o, f(x
o)):
y − f(
xo) = f'(
xo)*(
x −
xo)
jak widzisz ... masz we wzorze dwie zmienne niezależne: x
o i x ... nie możesz ich (obu)
zapisać jako jedna i ta sama zmienna

Jeżeli chcesz napisać P(x, f(x)) ... proszę bardzo, ale wtedy
x nie może występować, musi
być inne oznaczenie tej zmiennej co przełoży się na mylną postać stycznej i ogólne zaplątanie
się w temacie.
16 mar 12:47
salamandra: Już po Twoim wpisie 00:31 to widziałem

ale domyślam się, że jak trafię ponownie takie
zadanie to najzwyczajniej o tym zapomnę

16 mar 12:48
salamandra: No właśnie nie wiem czemu się zaplątałem, bo nie miałem tego typu zagwostek przy realizacji
pochodnej i pisania stycznych

16 mar 12:49
wredulus_pospolitus:
Bo przy zadaniach na wyznaczanie stycznych, nie miałeś zadania optymalizującego −−− miałeś
podane współrzędne punktu (czyli konkretną wartość w),
bądź miałeś konkretną postać pochodnej i sprawdzałeś współrzędne punktu styczności.
Bo przy wstępnych zadaniach na pochodne nie miałeś zadań optymalizacyjnych

Innymi słowy −−− nie miałeś jeszcze zadania w którym wyznaczasz ogólny wzór dla CAŁEJ RODZINY
stycznych do wykresu f(x).
16 mar 12:54
Eta:
Wredulus ... idź na

16 mar 13:01
wredulus_pospolitus:
Byłem

Pierwsza dzisiejszego dnia

16 mar 13:18
Eta:
To sukces! ( ja do takiego jeszcze nie doszłam

16 mar 13:21
wredulus_pospolitus:
nie wiem czy sukces ... skoro podniosłem się z wyrka pół godziny temu

16 mar 13:22
Eta: 
16 mar 13:22
wredulus_pospolitus:
2 tygodnie 'w izolacji' powoduje, że trochę mi się godziny poprzestawiały

16 mar 13:26
Eta:
Ja każdego dnia

do 11

16 mar 13:28
wredulus_pospolitus:
Niestety − nie mam tak dobrze na co dzień, więc teraz 'szaleję'

16 mar 13:30
an:
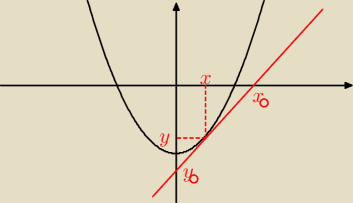
y=x
2−1⇒y'=2x
liczę pole bez równania stycznej, i to chyba miał na myśli autor
| | 1 | | 1 | | x2−1 | | 9x3 | | 3x | | 1 | |
P= |
| x0*y0= |
| (x+ |
| )(x2−1+2x2)= |
| − |
| + |
| |
| | 2 | | 2 | | 2x | | 4 | | 2 | | 4x | |
27x
4−6x
2−1=0
| | √3 | | √3 | |
x1= |
| lub x1= |
| x3,4 nierzeczywiste |
| | 3 | | 3 | |
.....
17 mar 01:04
 W jakim punkcie paraboli o równaniu y=x2−1 należy poprowadzić styczną, aby trójkąt ograniczony
tą styczną i osiami układu współrzędnych miał najmniejsze pole?
y=x2−1
P=(x,x2−1)
f'(x)=2x
Jakaś podpowiedź?
W jakim punkcie paraboli o równaniu y=x2−1 należy poprowadzić styczną, aby trójkąt ograniczony
tą styczną i osiami układu współrzędnych miał najmniejsze pole?
y=x2−1
P=(x,x2−1)
f'(x)=2x
Jakaś podpowiedź?


 krok 4:
Pole(x) = a*b = ....
krok 5:
Pole'(x) = ...
krok 4:
Pole(x) = a*b = ....
krok 5:
Pole'(x) = ...

 ale dlaczego piszesz x0, a nie po prostu x?
ale dlaczego piszesz x0, a nie po prostu x?
 ) wartość zmiennej 'x'
) wartość zmiennej 'x'
 żeby Ci się nie 'pojebało' ze zmienną 'x' występującą w równaniu prostej
P(w,w2−1)
styczna ma równanie y = 2w*x − (w2 + 1)
weźmy, punkt P(0,−1)
y = 2*0*x − (0 + 1) −−−> y = −1 zgadza się
weźmy punkt P(1, 0)
y = 2*1*x − (1 + 1) −−−−> y = 2x − 2 także się zgadza
weźmy punkt P(1/2 , −3/4)
y = x − 5/4
żeby Ci się nie 'pojebało' ze zmienną 'x' występującą w równaniu prostej
P(w,w2−1)
styczna ma równanie y = 2w*x − (w2 + 1)
weźmy, punkt P(0,−1)
y = 2*0*x − (0 + 1) −−−> y = −1 zgadza się
weźmy punkt P(1, 0)
y = 2*1*x − (1 + 1) −−−−> y = 2x − 2 także się zgadza
weźmy punkt P(1/2 , −3/4)
y = x − 5/4

 B=(0,0)
C=f(0)=w2−1
A=(w,0)
|AB|=w
|BC|=w2−1
B=(0,0)
C=f(0)=w2−1
A=(w,0)
|AB|=w
|BC|=w2−1
 czemu |AB| = w
czemu |AB| = w  z jakiej racji
z jakiej racji  już nawet na Twoim rysunku z 23:57
P(w, w2 − 1) ....
punkt A jest gdzieś w okolicach (3,0) ... więc co ... w = 3
już nawet na Twoim rysunku z 23:57
P(w, w2 − 1) ....
punkt A jest gdzieś w okolicach (3,0) ... więc co ... w = 3  nie ... w ≈ 1/3 (patrząc na
rysunek)
punkt C także źle wyznaczony ... f(0) = − (w2 + 1)
nie ... w ≈ 1/3 (patrząc na
rysunek)
punkt C także źle wyznaczony ... f(0) = − (w2 + 1)


 Pamiętaj ,że ze względu na parzystość funkcji
są dwa takie punkty P symetryczne względem osi OY
Pamiętaj ,że ze względu na parzystość funkcji
są dwa takie punkty P symetryczne względem osi OY



 ?
?

 ponad godzinę straciłem nad tym dziadostwem...
ponad godzinę straciłem nad tym dziadostwem...
 Czy wtedy wykres pochodnej będzie wyglądał tak?
Czy wtedy wykres pochodnej będzie wyglądał tak?




 Jeżeli chcesz napisać P(x, f(x)) ... proszę bardzo, ale wtedy x nie może występować, musi
być inne oznaczenie tej zmiennej co przełoży się na mylną postać stycznej i ogólne zaplątanie
się w temacie.
Jeżeli chcesz napisać P(x, f(x)) ... proszę bardzo, ale wtedy x nie może występować, musi
być inne oznaczenie tej zmiennej co przełoży się na mylną postać stycznej i ogólne zaplątanie
się w temacie.
 ale domyślam się, że jak trafię ponownie takie
zadanie to najzwyczajniej o tym zapomnę
ale domyślam się, że jak trafię ponownie takie
zadanie to najzwyczajniej o tym zapomnę 

 Innymi słowy −−− nie miałeś jeszcze zadania w którym wyznaczasz ogólny wzór dla CAŁEJ RODZINY
stycznych do wykresu f(x).
Innymi słowy −−− nie miałeś jeszcze zadania w którym wyznaczasz ogólny wzór dla CAŁEJ RODZINY
stycznych do wykresu f(x).

 Pierwsza dzisiejszego dnia
Pierwsza dzisiejszego dnia 




 do 11
do 11 

 y=x2−1⇒y'=2x
liczę pole bez równania stycznej, i to chyba miał na myśli autor
y=x2−1⇒y'=2x
liczę pole bez równania stycznej, i to chyba miał na myśli autor