stereometria
salamandra: Punkty A=(1,−2), D=(−2,2) są kolejnymi wierzchołkami trapezu ABCD . Prosta x+2y−7=0 jest osią
symetrii tego trapezu.
Wyznacz współrzędne pozostałych wierzchołków tego trapezu, a następnie oblicz objętośc bryły
otrzymanej w wyniku obrotu trapezu wokół krótszej podstawy.
A=(1,−2)
D=(−2,2)
x+2y−7=0
Moje rozumowanie jest takie:
Podstawa na której leży założmy punkt D, prosta ta, jest prostopadła do osi symetrii, więc jej
a=2
Na tej prostej leży punkt D, czyli y=ax+b
2=−2*2+b
b=6
y=2x−6
punkt przecięcia się prostych wyznaczy środek podstawy.
punkt C leży na tej prostej i jest jednakowo odległy od tego środka co punkt D. itd?
18 mar 01:57
wredulus_pospolitus:
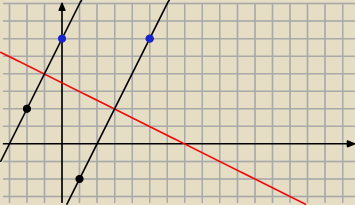
Dokładnie
18 mar 02:04
salamandra: No to nie wyszło mi z tego

18 mar 02:04
salamandra: | | 19 | | 38 | | 30 | | 8 | |
y=2* |
| −6= |
| − |
| = |
| |
| | 5 | | 5 | | 5 | | 5 | |
CS=DS
Wybacz jak jakieś błędy są w zapisie, pisze z telefonu
18 mar 02:08
wredulus_pospolitus:
y = 2x +6 <−−− ta prosta przechodzi przez punkt D (patrz mój rysunek)
18 mar 02:16
wredulus_pospolitus:
wyliczyłeś b =
+ 6
i do wzoru y = 2x + b podstawiłeś −6

i tak powstało y = 2x
− 6

18 mar 02:17
wredulus_pospolitus:
Nauczka na przyszłość −−− wyliczyłeś prostą ... podstaw współrzędne punktu/−ów i sprawdź czy
się zgadza

18 mar 02:18
salamandra: Niech będzie, że to przez godzinę...

18 mar 02:19
wredulus_pospolitus:
A nie przez te pół litra vódki obalone pół godziny temu

No dobra ... niech Ci będzie, ze to
przez godzinę
18 mar 02:20
salamandra: Wtedy na pewno nie byłoby takiego błędu

(sprawdzone)
Dokończę rankiem, dzięki za potwierdzenie rozumowania
18 mar 02:21
wredulus_pospolitus:
i szczerze mówiąc to nie wiem co Ty podstawiłeś w pierwszej linijce rozwiązania o 02:08
czyżbyś tam o 'x' nie zapomniał przypadkiem

18 mar 02:22
salamandra: Zapomniałem, zapomniałem, mówiłem ze z telefonu pisze

18 mar 02:22
wredulus_pospolitus:
No i punkt C
NA PEWNO nie ma takich współrzędnych (chodzi o drugą współrzędną) −−− nie
tą prostą wziąłeś.
Pamiętaj: Piłeś? Nie rób zadań z matematyki

18 mar 02:23
salamandra: Tak, racja, za dużo chciałem w myśli zrobić zamiast sobie rozpisać i byłem przekonany, że to ta
prosta „moja”, a nie oś symetrii , dzięki raz jeszcze
18 mar 02:25
salamandra: Czy odległość środków podstaw wyznaczy mi promień bryły powstałej w wyniku obrotu wokół
krótszej podstawy?
18 mar 13:32
salamandra:
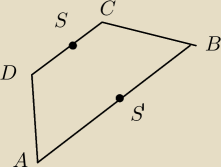
te współrzędne mi wyszły poprawnie
S=(−1,4)
S'=(3,2)
18 mar 13:35
Bleee:
Tak... Odległość pomiędzy środkami jest równa promieniowi bryły powstałej z obrotu tego trapezu
wokół podstawy (czy 5o krótszej, czy to dłuższej)
18 mar 13:39
salamandra:
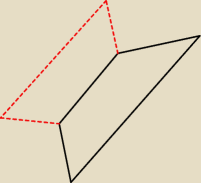
takie coś powstanie? nie umiem sobie tego wyobrazić
18 mar 13:44
wredulus_pospolitus:
tak ... powstanie walec o wysokości |AB| z wyciętymi dwoma stożkami (na podstawach) o łącznych
wysokościach |AB| − |CD|
18 mar 13:45
wredulus_pospolitus:
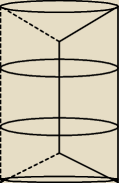
18 mar 13:46
salamandra: Ostro, czyli zeby policzyć objętość tego to liczę Vwalca, i odejmuję objętości tych dwóch
stożków?
18 mar 13:47
wredulus_pospolitus:
Tak i dodatkowo zauważ, że:
V
walca = πr
2*H = π(h
trapezu)
2 * |AB|
| | 1 | |
Vstożka 1 + Vstożka 2 = |
| (πr2*H1 + πr2*H2) = |
| | 3 | |
= π(h
trapezu)
2 * ( H
1 + H
2 ) = π(h
trapezu)
2 * ( |AB| − |CD| )
18 mar 13:50
salamandra: | | 1 | |
wysokość stożka (jednego) to będzie |
| *(AB−CD)? |
| | 2 | |
18 mar 13:53
salamandra: wyszło

dzieki
18 mar 14:09
wredulus_pospolitus:
Tak ... tutaj trapez jest równoramienny więc taka będzie wysokość każdego ze stożków ... ale
gdyby to nie był równoramienny ... to po prostu w ten sposób (co napisałem) nie trzeba
wyznaczać wysokości każdego z tych stożków (pamiętasz poprzednie zadania gdzie Ci to
pokazywałem).
18 mar 14:27
salamandra: Nie, nie kojarzę, abym miał zadanie z obrotem trapezu, może nie mi tłumaczyłeś?
18 mar 14:28
18 mar 14:37
salamandra: Tamto było łatwiejsze

nie potrafię nigdy zapamiętać żeby użyć przyrównania pól, tak jak
zrobiles to w tamtym, dlatego te moje „długie” rozwiązania maja miejsce
18 mar 14:42
wredulus_pospolitus:
Chodzi oto, że i w tym zadaniu można było skorzystać z liczenia objętości obu stożków
jednocześnie biorąc sumę ich wysokości (tak jak to było w tamtym zadaniu).
Tutaj szczęśliwie trapez był równoramienny więc wysokości ładnie się podzieliły, ale gdyby było
tak jak w tamtym zadaniu to znowu byś siedział i niepotrzebnie tracił parę minut na obliczenie
wysokości każdego z nich.
18 mar 14:50
salamandra:
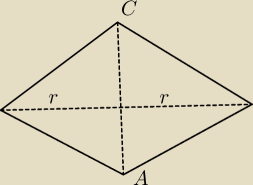
| | 1 | |
Czyli mając taką klepsydrę (dwa stożki) to ich objętość to |
| *πr 2*AC  i nie muszę |
| | 3 | |
rozpatrywać dwóch oddzielnie?
18 mar 14:52
wredulus_pospolitus:
Dokładnie

18 mar 14:53
salamandra: to bajeczka

18 mar 14:53
wredulus_pospolitus:
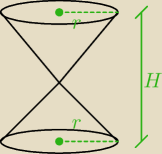
I tu także
18 mar 14:55
wredulus_pospolitus:
A W tym zadaniu de facto miałeś to co napisałem o 14:55 (tylko te dwa stożki w zadaniu się
nie stykają)
18 mar 14:55
salamandra: A co właśnie jeśli by nie był trapez równoramienny?
18 mar 15:01
salamandra: zresztą to że jest oś symetrii od razu sugeruje, że jest równoramienny, racja?
18 mar 15:01
wredulus_pospolitus:
nie sugeruje tylko o tym przesądza

18 mar 15:03
 Dokładnie
Dokładnie

 i tak powstało y = 2x − 6
i tak powstało y = 2x − 6 


 No dobra ... niech Ci będzie, ze to
przez godzinę
No dobra ... niech Ci będzie, ze to
przez godzinę
 (sprawdzone)
Dokończę rankiem, dzięki za potwierdzenie rozumowania
(sprawdzone)
Dokończę rankiem, dzięki za potwierdzenie rozumowania



 te współrzędne mi wyszły poprawnie
S=(−1,4)
S'=(3,2)
te współrzędne mi wyszły poprawnie
S=(−1,4)
S'=(3,2)
 takie coś powstanie? nie umiem sobie tego wyobrazić
takie coś powstanie? nie umiem sobie tego wyobrazić

 dzieki
dzieki
 nie potrafię nigdy zapamiętać żeby użyć przyrównania pól, tak jak
zrobiles to w tamtym, dlatego te moje „długie” rozwiązania maja miejsce
nie potrafię nigdy zapamiętać żeby użyć przyrównania pól, tak jak
zrobiles to w tamtym, dlatego te moje „długie” rozwiązania maja miejsce

 i nie muszę
i nie muszę

 I tu także
I tu także
