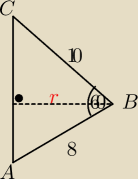
 W trójkącie ABC, AC=7, BC=8, zaś ∡ABC=60. Oblicz objętość bryły powstałej z obrotu trójkąta ABC
wokół prostej zawierającej bok AC.
Chcę tylko wiedzieć czy promień będzie tam gdzie narysowałem, bo zawsze mam problem z
wyobrażeniem sobie gdzie powstaje ten okrąg?
W trójkącie ABC, AC=7, BC=8, zaś ∡ABC=60. Oblicz objętość bryły powstałej z obrotu trójkąta ABC
wokół prostej zawierającej bok AC.
Chcę tylko wiedzieć czy promień będzie tam gdzie narysowałem, bo zawsze mam problem z
wyobrażeniem sobie gdzie powstaje ten okrąg?


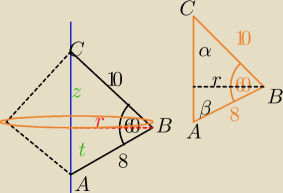 Nie wiem czy dobrze tutaj kombinuję,
Nie wiem czy dobrze tutaj kombinuję,
| 1 | ||
|AC|2=64+100−160* | (tw cosinusów) | |
| 2 |
| 2√21 | 8 | ||||||||
= | |||||||||
| sinα |
| 4 | 4√21 | 2√21 | ||||
sinα= | = | = | ||||
| 2√21 | 42 | 21 |
| 10 | 2√21 | ||||||||
= | |||||||||
| sinβ |
|
| 5√21 | ||
sinβ= | ||
| 42 |
| r | 10 | ||
= | |||
| sinα | sin90 |
| r | |||||||
=10 | |||||||
|
| 2√21 | 20√21 | |||
r=10* | = | |||
| 21 | 21 |
| 20√21 | ||
( | )2+z2=100 | |
| 21 |
| 10√357 | ||
z= | ||
| 21 |
| 4√1239 | ||
t= | ||
| 21 |
| 10 | 2√21 | ||||||||||||
w | = | ||||||||||||
| sinβ |
|

 z i t NIE SĄ CI POTRZEBNE
z i t NIE SĄ CI POTRZEBNE  zauważ, że masz do obliczenia
zauważ, że masz do obliczenia
| 1 | 1 | 1 | 1 | |||||
V = V1 + V2 = | πr2*z + | πr2*t = | πr2*(z+t) = | πr2*|AC|  | ||||
| 3 | 3 | 3 | 3 |
| a*b*sin60o | ||
krok 2: wyznaczasz pole trójkąta ze wzoru: PΔ = | ||
| 2 |
| |AC|*h | ||
krok 3: wyznaczasz h = r ze wzoru na pole PΔ = | ||
| 2 |
| 2√21 | 8 | ||||||||
= | |||||||||
| sinα |
| 4√3 | 4√63 | 2√63 | 6√7 | 2√7 | ||||||
sinα= | = | = | = | = | ||||||
| 2√21 | 42 | 21 | 21 | 7 |
| 10 | 2√21 | ||||||||
= | |||||||||
| sinβ |
|
| 5√3 | ||
sinβ= | ||
| 2√21 |
| 5√7 | ||
sinβ= | ||
| 14 |
| r | 10 | ||
= | |||
| sinα | sin90 |
| r | |||||||
=10 | |||||||
|
| 20√7 | ||
r= | ||
| 7 |
| 20√7 | ||
( | )2+z2=100 | |
| 7 |
| 10√21 | ||
z= | ||
| 7 |
| 20√7 | ||
( | )2+t2=64 | |
| 7 |
| 4√21 | ||
t= | ||
| 7 |
| 2800 | ||
r2= | ||
| 49 |
| 1 | 2800 | 10√21 | 1 | 400 | 4000√21 | |||||||
V1= | π* | * | = | π* | *10√21= | π | ||||||
| 3 | 49 | 7 | 3 | 49 | 147 |
| 1 | 2800 | 4√21 | 1 | 400 | 1600√21 | |||||||
V2= | π* | * | π* | *4√21= | π | |||||||
| 3 | 49 | 7 | 3 | 49 | 147 |
| 4000√21 | 1600√21 | 5600√21 | 800√21 | |||||
Vc= | π+ | π= | π= | π | ||||
| 147 | 147 | 147 | 21 |
 przyznam po prostu, że jak zobaczyłem, że te
dwa stożki będą miały inną wysokość, to myślałem, że muszę właśnie je oddzielnie rozpatrzeć,
ale wyszło
przyznam po prostu, że jak zobaczyłem, że te
dwa stożki będą miały inną wysokość, to myślałem, że muszę właśnie je oddzielnie rozpatrzeć,
ale wyszło
| |||||||||||
PΔ= | =20√3 | ||||||||||
| 2 |
| 1 | ||
PΔ=AC*h* | ||
| 2 |
| 1 | ||
20√3=2√21*h* | ||
| 2 |
| 20√63 | |
=h | |
| 21 |
| 60√7 | |
=h | |
| 21 |
| 20√7 | |
=h | |
| 7 |
| 1 | 20√7 | 1 | 2800 | 800√21 | ||||||
V= | *π*( | )2*2√21 = | π* | *2√21= | ||||||
| 3 | 7 | 3 | 49 | 21 |


 No szczerze mówiąc przeglądając matury nie widziałem takiego zadania, ale może dlatego ze
ostatnio jak je przeglądałem to nie miałem jeszcze opanowanej stereometrii wiec je opuszczałem
No szczerze mówiąc przeglądając matury nie widziałem takiego zadania, ale może dlatego ze
ostatnio jak je przeglądałem to nie miałem jeszcze opanowanej stereometrii wiec je opuszczałem