stereometria salamandra: Dany jest sześcian o krawędzi a. Środki jego ścian łączymy kolejno odcinkami. środki ścian otrzymanego ośmiościanu znowu łączymy odcinkami itd. Oblicz sumę objętości wszystkich otrzymanych w ten sposób sześcianów. Mógłby mi to ktoś narysować? W zeszycie mi się zlewa wszystko jak próbuję to narysować

Eta: https://matematykaszkolna.pl/forum/271994.html

Eta: https://forum.zadania.info/viewtopic.php?t=77765 i analizuj rozwiązanie

salamandra: Jak narysować ośmiościan? Dwa ostrosłupy prawidłowe czworokątne sklejone?

Eta: Dokładnie tak

salamandra: A co mi daje ta odległość ścian równoległych? chyba nie bardzo w ogóle rozumiem polecenie, bo w którym miejscu ja otrzymuję sześciany?

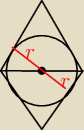
salamandra: z tego coś muszę wyznaczać? nie wiem o co chodzi w tym zadaniu

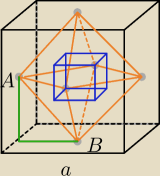
Saizou : Trzeba ustalić jak postępują długości boków sześcianu. Najpierw ustalmy jak długa jest krawędź ośmiościanu

	√2
|AB|=		a
	2

Podpowiedź: Znajdź długość odcinka, który łączy środki ścian ostrosłupa prawidłowego czworokątnego o długości krawędzi bocznej k.

salamandra: A co reprezentuje ten niebieski sześcian? Skąd on się wziął?

Saizou : "środki ścian otrzymanego ośmiościanu znowu łączymy odcinkami" z tego powstanie sześcian

salamandra: A ten wierzchołek sześcianu (oznaczając uniwersalnie to byłby B’ dlaczego jest jakby na wierzchołku ostrosłupa, skoro łączymy ze środkami ścian?

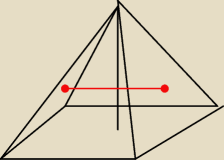
salamandra: mam znaleźć ten odcinek? czyli krawędź niebieskiego sześcianu?

salamandra: hm, ta odległośc która zaznaczyłem to będzie PRZEKĄTNA tego niebieskiego sześcianu i to będzie średnia kuli wpisanej w ostrosłup prawidłowy czworokątny?

Saizou : Nie, ty połączyłeś środki przeciwnych ścian, a mają być sąsiednie

salamandra: Tak, tak, dlatego post 22:08 jest aktualny

Saizou :

1   h 3		h
	=
x		2√3k

	2√3
x=		k
	3

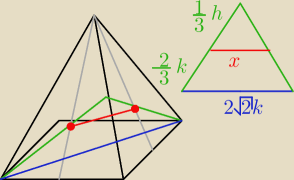
i dalej sam

salamandra: Zielone odcinki na ostroslupie to wysokość ściany bocznej?

Saizou : Rozumiem środek ściany jako punkt przecięcia się wysokości. Ściany boczne są trójkątami równobocznymi

salamandra: Aa, i dlatego ze to równoboczne to dzieli wysokość w stosunku 2:1? To powinno być w końcu 2/3 h czy 2/3k? Bo napisałeś 2/3k i 1/3h?

Saizou :

	2
tak, tam jest literówka		h
	3

salamandra:

	a√2
hm, skoro (wszystkie?) krawędzie ostrosłupa mają długość		, to przekątna podstawy
	2

	a√2*√2		2a
ostrosłupa (niebieski odcinek) powinien mieć		=		=a?
	2		2

skąd to 2√2k?,a później w proporcjach 2√3k?

Saizou : żeby mieć mniej pierwiastków, to założyłem sobie, że

√2
	a=2k
2

przekątna podstawy to 2√2k wysokości nie muszę liczyć, bo się skróci PS. Zmieniłem komputer i teraz uczę się pisać (zabrali mi klawiaturę numeryczną)

salamandra: Czyli to co powiedziałem jest poprawne? że niebieski odcinek to byłby a?

Saizou :

salamandra:

1   h 3		h
	=
x		a

	1
xh=		h*a/ : h
	3

	1
x=		a?
	3

Saizou : no tak i teraz

	1		27
S=a3		=		a3
	1   1−   27		26

salamandra: a jaką mamy pewność, że każdy będzie się tak zachowywał, nie musiałbym co najmniej trzech zbadać?

Saizou :

	1
nie musisz, niech teraz		a=p i powtarzamy rozumowanie
	3

V₁=a³

	1
V2=(		)3
	3

	1
V3=(		)3
	9

....

salamandra: ok, dzięki wielkie

Saizou : Ciekawe zadanko

salamandra: tak ciekawe, że od 17−tej nad nim utknąłem i już nic innego nie ruszyłem

Saizou : Wiesz, o wiele więcej wnosi takie zadanie, które wymaga więcej zastanowienia niż kolejne zrobione z automatu

salamandra: tak, tylko powiem Ci szczerze, że teraz przepisuję to do zeszytu i nadal nie potrafię tego narysować te środki mi się zlewają cały czas

Saizou : To zrób dwa rysunki. Jeden osmioscianem wpisanym w sześcian, a drugi sześcian wpisany w ośmiościan

salamandra: no właśnie tego ośmiościanu nie potrafię wpisać w ten sześcian

Saizou : Zrób tak że zaznacz środki boków ścian które nie są podstawami i je połącz w kwadrat (w perspektywie jakiś rownoleglobok to będzie), a dopiero później połącz z środkami postaw

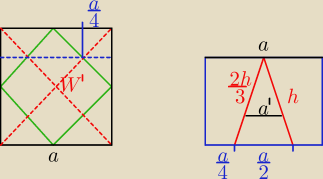
an: Ściany ośmiościanu trójkąty równoboczne Przecinamy sześcian płaszyzną na której leży "podstawa" ostrosłupa otrzymujemy przekrój rys I Następnie robimy przekrój płaszczyzną zawierającą wysokości dwu sąsiednich ścian bocznych ostrosłupa otrzymujemy przekrój rys II. Wiemy, że środek ściany bocznej leży na 1/3 jej wysokości, gdyż jest to trójkąt równoboczny. Z proporcji

a/2		a'		a		1
	=		⇒ a'=		⇒ q=		itd.
h		2h/3		3		33

Jak widać zadanie "banalne", trochę wyobraźni przestrzennej i odpowiednie rysunki, to podstawa ogólnie geometrii.

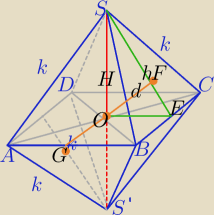
Mila: a− długość krawędzi sześcianu, w który wpisano powyższy ośmiokąt foremny p₁=a√3− długość przekątnej wyjściowego sześcianu

	a√2
k=		− długość krawędzi ośmiościanu ( to obliczyłeś wcześniej).
	2

1) |OF|=d 2d− Odległość środków ciężkości równoległych ścian ośmiościanu jest równa przekątnej sześcianu wpisanego w ten ośmiokąt.

	√2k		k√3
W ΔSOE: H=		, h=
	2		2

1		1		1
	H*		k=		h*d⇔
2		2		2

	k*√6
d=
	6

=======

	2k√6		√6		a√2		√6
|GF|=		=k*		=		*
	6		3		2		3

	√3
|GF|=		a= p2
	3

	p2		1
2) sześciany są figurami podobnymi⇔		=
	p1		3

V2		p2
	=(		)3
V		p1

	1
V2=		V
	27

objętości są wyrazami ciągu geometrycznego , gdzie a₁=a³

	1
q=
	27

( możesz obliczyć p₃ wg wzorów j.w)

	a3		27a3
3) S=		=
	1   1−   27		26

=====================

salamandra: