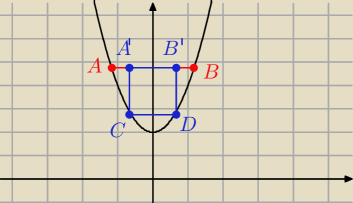
optymalizacja salamandra: Rozważamy wszystkie prostokąty, których dwa wierzchołki leżą na odcinku AB, gdzie A=(−1,4) i B=(1,4), a pozostałe dwa na paraboli o równaniu y=2x²+2. Wyznacz wymiary tego z prostokątów, który ma największe pole. Oblicz to pole. A=(−1,4) B=(1,4) C(−x, 2x²+2) D=(x,2x²+2) A'=(−x,4) B'=(x,4) x∊(0;1) |A'B'|=2x |A'C'|=√(−x+x)²+(2x²+2−4)² = √(2x²−2)² = |2x²−2|=2x²−2 (tutaj chyba mam błąd, ale nie wiem jak to przekształcić) P(x)=2x*(2x²−2)=4x³−4x² P'(x)=12x²−4 P'(x)=0 ⇔ 12x²−4 = 0 12x²=4

	1
x2=
	3

	−√3		√3
x=		v x=
	3		3

Saizou : Długość odcinka A'C, to po prostu różnica wartości tych punktów, czyli A'C=4−(2x²+2)=−2x²+2 U ciebie skoro x∊(0, 1), to |2x²−2| = −2x+2

Eta: https://matematykaszkolna.pl/forum/373629.html bo nie chce mi się 150 razy pisać

salamandra: Dla mnie nie zrobisz wyjątku? Saizou, a jaka jest różnica czy zapiszę (2x+2−4) czy 4−(2x²+2), myślałem, że to nie ma znaczenia

salamandra: Tak jakbym miał A(2,4) B(−1,3) No to nieważne czy zapiszę AB²=(−1−2)²+(3−4)² czy (2−(−1))²+(2−3)²?

salamandra: Ok, już czaję, nie zauważyłem tego że napisałem "U ciebie...."

salamandra: że napisałeś*

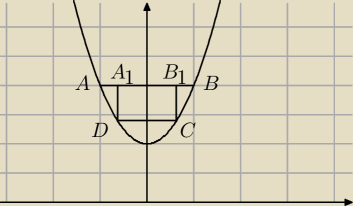Saizou : A₁=(−x, 4) B₁=(x, 4) C=(x, 2x²+2) D=(−x,2x²+2) dla x∊(0,1) |A₁B₁|=2x |A₁D|=4−(2x²+2)=−2x²+2 P(x)=2x(−2x²+2)=−4x³+4x P'(x)=−12x²+4=0

	√3
x=
	2

P''(x)=−24x

	√3		√3
P''(		)<0 zatem w x=		jest maksimum
	2		2

Saizou : poprawka

	√3
x=
	3

salamandra: Już mi wyszło, ale dzięki

Eta:

salamandra:

Eta: To piwo z "koroną" ( nie skorzystam

salamandra: trzeba się uodpornić

Eta:

Saizou : akurat alkohol osłabia odporność xd

salamandra: "z koroną" nie