Optymalizacja, funkcja Blabla: Rozważmy wszystkie prostokąty,których dwa wierzchołki leżą na odcinku AB, gdzie A=(−1,4) i B=(1,4) a pozostałe dwa na paraboli o równaniu y=2x² + 2. Wyznacz wymiary tego prostokąta, który ma największe pole. Oblicz to pole. Problem mam w wyznaczeniu długości y. Obliczyłem że jeden bok powinien mieć 2x a drugiego nie jestem w stanie obliczyć... Wiem, że muszę uwzględnić to 2x² + 2 ale nie wiem jak

Blee: A czymze jest ten tajemniczy x u ciebie?

Blabla: x jest jedną z długości prostokąta, i żeby wyliczyć drugi bok potrzebuje uzależnić z y, x

Blabla: *2x

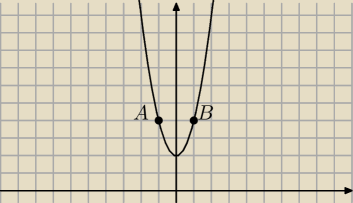
piotr: Kłopot w tym, że punkty A i B leżą na danej paraboli.

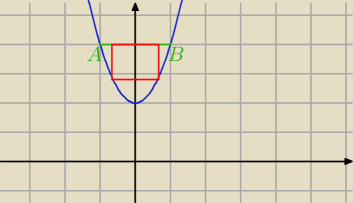
PW: Zgoda, podstawą prostokąta będzie więc odcinek "mniejszy" − zawarty w AB.

PW: Parabola jest symetryczna względem osi OY, tak więc jeżeli jeden z wierzchołków prostokąta leży na paraboli i ma współrzędne x, y (0<x<1, 2<y<4), to drugi ma współrzędne −x i y. Współrzędne są związane zależnością y = 2x²+2, zatem leżące na paraboli wierzchołki to (−x, 2(−x)²+2) i (x, 2x²+2), x∊(0, 1). Prostokąt ma wymiary (2x) na (4−y), pole P prostokąta wyraża się wzorem P(x)=2x(4−y), x∊(0, 1), P(x)=8x−2xy, x∊(0, 1) P(x)=8x−2x(2x²+2) P(x)=4x−4x³ P(x)=4(x−x³), x∊(0, 1)

	1
P'(x)=4(1−3x2), P'(x)=0⇔x=		,
	√3

	1		1		1		8
Pmax=P(		)=4		(1−		)=		.
	√3		√3		3		3√3

	2		4
Wymiary prostokąta o maksymalnym polu to 2x=		na 4−(2x2+2)=		.
	√3		3