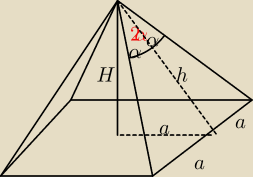
stereometria salamandra: Pole ściany bocznej ostrosłupa prawidłowego czworokątnego jest równe S. Kąt płaski przy wierzchołku ma miarę 2α. Obliczyć objętość ostrosłupa.

	a*h
S=		/ * 2
	2

2S=a*h

2S
	=a
h

	a
tgα=
	h

tgα*h=a

2S
	=tgα*h / * h
h

2S=tgα*h²

2S
	=h2
tgα

	2S
h=√
	tgα

	a
tgα=
	h

tgα*h=a

	a
h=
	tgα

2S
	=a
2S   √   tgα

	4S
2a=
	2S   √   tgα

	16S2
Pp=(2a)2 =
	2S   tgα

	tgα		16S*tgα
16S2*		=		=8S*tgα = Pp
	2S		2

H²+a²=h²

	2S		4S2		2S		tgα		2S
H2=		−		=		−4S*		=		−2S*tgα=
	tgα		2S   tgα		tgα		2		tgα

	2S		2S*tg2α		2S−2S*tg2α
=		−		=
	tgα		tgα		tgα

	2S−2S*tg2α
H=√
	tgα

	1		2S−2S*tg2α
V=		*8S*tgα*√
	3		tgα

	4
Odpowiedź to:		√S3*tgα(1−tg2α)
	3

Popełniłem gdzieś błąd?

salamandra:

	a
Nie wiem dlaczego książka sugeruje, że tgα=
	2h

Jerzy:

	a   2		a
tgα =		=
	h		2h

salamandra: Jerzy, ja założyłem, że bok podstawy to 2a

salamandra:

	2a*h
Ok, wiem, powinienem był napisać S=		...
	2

salamandra: Od nowa:

	2a*h
S=		= a*h
	2

	a
tgα=
	h

tgα*h=a S=tgα*h*h = tgα*h²

S
	=h2
tgα

	S
h=√
	tgα

	S		S*tg2α
a=tgα*√		= √		= √S*tgα
	tgα		tgα

2a=2*√S*tgα=√4S*tgα Pp=4S*tgα H²+a²=h²

	S
H2+S*tgα=
	tgα

	S
H2=		−Stgα
	tgα

	S		S*tg2α		S−S*tg2α		S(1−tg2α)
H2=		−		=		=
	tgα		tgα		tgα		tgα

	S(1−tg2α)
H=√
	tgα

	1		S(1−tg2α)		4		S(1−tg2α)
V=		*4S*tgα*√		=		*S*tgα*√		=
	3		tgα		3		tgα

	4		S3*tg2α(1−tg2α)		4
=		*√		=		√S3*tgα(1−tg2α)
	3		tgα		3

Saizou : https://matematykaszkolna.pl/forum/397635.html tutaj to rozwiązywałem niedawno

salamandra: Nawet „wzrokowo” pamietam wyszło na szczęście

Patryk: Powiem Ci szczerze, że dziwię się Tobie, że chcę Ci sie tyle pisać tyle na forum, i to dwa razy takie długie rozwiązanie

salamandra: Wole tak, niż żeby ktoś się domyślał co napisałem w zeszycie