objetosc ostroslupa michaeli19: W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość b, a kąt miedzy równymi bokami podstawy ma miarę α. Oblicz objętość tego ostrosłupa. wychodzi mi (b³ * sinα * √1−b²(1−cosα)² ) / 6 a wynik w podr to (√2b³ / 12) * sinα* √(1+2cosα)/(1+cosα)

wredulus_pospolitus: no super ... a chociaż byś pokazał swoje obliczenia

michaeli19: z tw. cosinusów obliczyłem a = b*√2−2cosα pole podstawy (b² * sinα)/2 promień okręgu opisanego na podstawie R R = b²(1−cosα) z tw. pitagorasa H² + R² = b² H = b√1−b²(1−cosα)² podstawiłem pod V = 1/3 * Ppodst * H

wredulus_pospolitus: pragnę dodatkowo zauważyć, że u Ciebie wychodzi b ≤ 1 a co jeszcze lepsze ... dla b = 1 i α = 90^o wychodzi V = 0 Więc raczej chyba jednak masz źle ... nie sądzisz

wredulus_pospolitus: Co to jest a Proszę pokazać jak wyszedł Ci R

michaeli19: pozostały bok trójkąta w podstawie oznaczyłem jako a R=abc/4Pp = ab² / 2b²sinα = a / 2sinα = b²(1−cosα)

a7: https://matematykaszkolna.pl/forum/389256.html

wredulus_pospolitus: zaprezentuj przejście:

a
	= b2(1−cosα)
2sinα

michaeli19: rzeczywiście, totalnie się zaplątałem

michaeli19: poprawilem blad z R i mi wyszlo po przeksztalceniu tak samo jak w linku od a7, dzieki

an:

	α
a=2bsin
	2

	α
c=bcos
	2

	b		b		b
h=√(b2cos2α/2−b2/4)=		√4cos2α/2−1=		√2(2cos2α/2−1)+1=		√2cosα+1
	2		2		2

	h*b		b2
PACE=		=		√2cosα+1
	2		4

	1		a		1		α		b2		b3		α
V=		2*		*PACE=		2bsin				√2cosα+1 =		sin
	3		2		3		2		4		12		2

√2cosα+1

	α		α		α		sinα		sinα
sinα=2sin		cos		⇒⇒cos		=		=		=
	2		2		2		α   2sin   2		√4−4sin2α/2

	sinα		√2sinα
=		=
	√2−(4sin2α/2−2)		√1+cosα)

	b3		α
V=		sin		√2cosα+1
	12		2

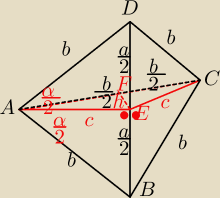
an: namieszało się z tego wklejania chciałem pokazać że można to zrobić z dwu osrosłupów powstałych z przecięcia zadanego ostrosłupa płaszczyzną, na której powstaje ich podstawa ΔACE

	sinα		sinα		sinα
sinα=2sinα/2cosα/2 ⇒sinα/2=		=		=		=
	2cosα/2		√4cos2α/2		√4−4sin2α/2

	sinα		√2sinα
=		=
	√2+(2−4sin2α/2)		√1+cosα

	√2b3		√2cosα+1
V=
	12		√1+cosα