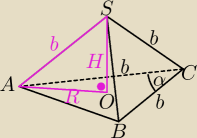
objętość ostrosłupa john: W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość b, a kąt między równymi bokami podstawy ma miarę α. Oblicz objętość tego ostrosłupa. Proszę o sprawdzenie bo chyba mam coś źle a nie wiem co: Na mocy tw cosinusów w trójkącie ABC: AB² = 2b² − 2b²cosα AB = b√2 − 2cosα korzystam z faktu, że spodek wysokości w ostrosłupie w którym krawędzie boczne mają równe długości znajduje się w środku okręgu opisanego na podstawie, więc na mocy tw. sinusów:

	b√2 − 2cosα
2R =
	sinα

	b√2 − 2cosα
R =
	2sinα

Aby obliczyć wysokość korzystam z tw. pitagorasa w trójkącie AOS:

	b2(2 − 2cosα)
H2 = b2 −
	4sin2α

	b√4sin2α + 2cosα − 2
H =
	2sinα

	1		b2sinα
Pp =		* b2 * sinα =
	2		2

	1		b3√4sin2α + 2cosα − 2
V =		* Pp * H =
	3		12

Mila: Jaki masz wynik w odpowiedzi, może przekształcono wyrażenie pod pierwiastkiem?

john: https://www.zadania.info/d414/5927816 chyba to trochę inne wyrażenia

Mila: Inna metoda rozwiązane. Spróbuję przeliczyc.

john:

	b3
@Mila zobacz, wpisałem mój wynik i wynik stamtąd bez		i wychodzą inne funkcje
	6

https://www.wolframalpha.com/input/?i=(sqrt(4sin%5E2(a)%2B2cos(a)-2))%2F2+%3D+sin(a%2F2)*sqrt(2cos(a)+%2B+1)

Mila: Masz dobrze.

john: To nie rozumiem, możesz pokazać przekształcenia? Jeśli nie są jakieś długie Dzięki

Mila: Jeszcze raz jutro przeliczę

john: okej

Mila: √4sin²x+2cosx−2=√4*4sin²(x/2)*cos²(x/2)+2*(1−2sin²(x/2)−2= =√16sin²(x/2)*cos²(x/2)+2−4sin²(x/2)−2= =√16sin²(x/2)*cos²(x/2)−4sin²(x/2)= =2sin(x/2)*√4cos²(x/2)−1=2sin(x/2)√4*^1+cosx₂−1= =2sin(x/2)*√2cosx+1

john: Dziękuję, tylko zastanawia mnie przedostatnie działanie, jak z cos²(x/2) otrzymać

	1+cosx
		?
	2

iteRacj@: Przekształć wzór na cosinus podwojonego kąta.

Eta: cos(2x)=cos²x−sin²x= cos²x−(1−cos²x)=2cos²x−1 to 1+cos(2x)=2cos²x to 1+cosx=2cos²(x/2) analogicznie 1−cosx=2sin²(x/2)

john: Dzięki raz jeszcze