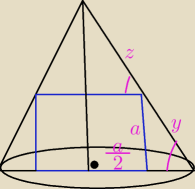
Tworząca stożka ma długość l i jest nachylona do płaszczyzny podstawy pod kątem α. W stożek ten
wpisano sześcian tak że cztery jego wierzchołki należą do powierzchni bocznej stożka zaś
cztery pozostałe należą do podstawy stożka. Znajdź długość krawędzi sześcianu.
Czy mogę to zrobić w następujący sposób? Bo podejrzanie mało obliczeń i nie wiem czy dobrze
zobrazowałem sytuacje na rysunku...
z + y = l
a −−> krawędź sześcianu
| a | ||
1) sin α = | ||
| y |
| a | ||
y = | ||
| sinα |
| ||||||||
2) cosα = | ||||||||
| z |
| 0,5a | ||
z = | ||
| cosα |
| a | 0,5a | ||
+ | = l | ||
| sinα | cosα |
| l | ||
a = | ||
| cosα + 0,5sinα |
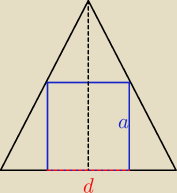rysunek nie odpowiada faktycznej sytuacji 
d −−− PRZEKĄTNA podstawy sześcianu
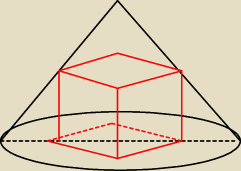trochę krzywo mi wyszedł ten sześcian ... ale mam nadzieję że widzisz teraz to.
