Twierdzenie odwrotne
AHQ:
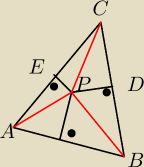
Dany jest trójkąt ABC oraz dowolny punkt P w jego wnętrzu. Oznaczmy przez D,
E, i F rzuty P na boki BC, CA i AB trójkąta ABC. Wykaz, ze:
BD
2 + CE
2 + AF
2 = DC
2 + EA
2 + FB
2
Czy twierdzenie odwrotne również jest prawdziwe? Tzn. czy jeżeli punkty D, E, F leżące
na bokach BC, CA, AB spełniają te równość, to czy musi istnieć punkt P, dla którego
są one rzutami na te boki?
Zapisałem tw. Pitagorasa dla małych Δ prostokątnych i wyznaczyłem odcinki potrzebne do
tezy − wszystko ładnie się skróciło. Jak pokazać (lub obalić) twierdzenie w przeciwną stronę ?
13 mar 11:50
13 mar 12:52
AHQ: Chodzi o to, że przy takich oznaczeniach punkt P znajduje się w wierzchołku C, czyli nie w jego
wnętrzu ?
13 mar 13:21
wredulus_pospolitus:
Tak ... twierdzenie w drugą stronę nie jest prawdziwe, bo można dobrać tak punkt P, aby
spełniał tą nierówność a nie był we wnętrzu trójkąta.
13 mar 13:39
AHQ: A gdyby punkt P nie musiał leżeć wewnątrz trójkąta, tylko w dowolnym punkcie na
płaszczyźnie, to tw. odwrotne byłoby prawdziwe nie ? Jak wtedy należałoby to pokazać ?
16 mar 12:32
AHQ: .
16 mar 17:25
wredulus_pospolitus:
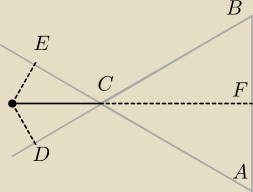
jeżeli rzuty na boki uznamy jako rzuty na przedłużenia boków to mamy powyższą sytuację
|AF|
2 = |BF|
2
|BD|
2 = |AE|
2
|CE|
2 = |CD|
2
dodajemy ... mamy równość daną w twierdzeniu.
Jeżeli natomiast nie będziemy tak rozpatrywać w taki sposób rzutów na boki, to dla P poza
trójkątem nie ma czegoś takiego jak rzut punktu na bok (nie na każdy bok) tegoż trójkąta.
Przykład zaprezentowany na trójkącie równobocznym, ale także i dla równoramiennego będziesz
miał powyższe równości.
Czy ta (ogólna) równość będzie działać dla dowolnego trójkąta i dowolnego umiejscowienia punktu
P ... nie wiem ... i nawet nie mam zamiaru tego sprawdzać.
16 mar 17:36
 Dany jest trójkąt ABC oraz dowolny punkt P w jego wnętrzu. Oznaczmy przez D,
E, i F rzuty P na boki BC, CA i AB trójkąta ABC. Wykaz, ze:
BD2 + CE2 + AF2 = DC2 + EA2 + FB2
Czy twierdzenie odwrotne również jest prawdziwe? Tzn. czy jeżeli punkty D, E, F leżące
na bokach BC, CA, AB spełniają te równość, to czy musi istnieć punkt P, dla którego
są one rzutami na te boki?
Zapisałem tw. Pitagorasa dla małych Δ prostokątnych i wyznaczyłem odcinki potrzebne do
tezy − wszystko ładnie się skróciło. Jak pokazać (lub obalić) twierdzenie w przeciwną stronę ?
Dany jest trójkąt ABC oraz dowolny punkt P w jego wnętrzu. Oznaczmy przez D,
E, i F rzuty P na boki BC, CA i AB trójkąta ABC. Wykaz, ze:
BD2 + CE2 + AF2 = DC2 + EA2 + FB2
Czy twierdzenie odwrotne również jest prawdziwe? Tzn. czy jeżeli punkty D, E, F leżące
na bokach BC, CA, AB spełniają te równość, to czy musi istnieć punkt P, dla którego
są one rzutami na te boki?
Zapisałem tw. Pitagorasa dla małych Δ prostokątnych i wyznaczyłem odcinki potrzebne do
tezy − wszystko ładnie się skróciło. Jak pokazać (lub obalić) twierdzenie w przeciwną stronę ?
 jeżeli rzuty na boki uznamy jako rzuty na przedłużenia boków to mamy powyższą sytuację
|AF|2 = |BF|2
|BD|2 = |AE|2
|CE|2 = |CD|2
dodajemy ... mamy równość daną w twierdzeniu.
Jeżeli natomiast nie będziemy tak rozpatrywać w taki sposób rzutów na boki, to dla P poza
trójkątem nie ma czegoś takiego jak rzut punktu na bok (nie na każdy bok) tegoż trójkąta.
Przykład zaprezentowany na trójkącie równobocznym, ale także i dla równoramiennego będziesz
miał powyższe równości.
Czy ta (ogólna) równość będzie działać dla dowolnego trójkąta i dowolnego umiejscowienia punktu
P ... nie wiem ... i nawet nie mam zamiaru tego sprawdzać.
jeżeli rzuty na boki uznamy jako rzuty na przedłużenia boków to mamy powyższą sytuację
|AF|2 = |BF|2
|BD|2 = |AE|2
|CE|2 = |CD|2
dodajemy ... mamy równość daną w twierdzeniu.
Jeżeli natomiast nie będziemy tak rozpatrywać w taki sposób rzutów na boki, to dla P poza
trójkątem nie ma czegoś takiego jak rzut punktu na bok (nie na każdy bok) tegoż trójkąta.
Przykład zaprezentowany na trójkącie równobocznym, ale także i dla równoramiennego będziesz
miał powyższe równości.
Czy ta (ogólna) równość będzie działać dla dowolnego trójkąta i dowolnego umiejscowienia punktu
P ... nie wiem ... i nawet nie mam zamiaru tego sprawdzać.