Dowód - geomteria
Witcher77: Dany jest trójkąt ABC oraz dowolny punkt P w jego wnętrzu. Oznaczmy przez D,
E, i F rzuty P na boki BC, CA i AB trójkąta ABC. Wykaz, ze:
BD2 + CE2 + AF2 = DC2 + EA2 + FB2
Czy twierdzenie odwrotne również jest prawdziwe? Tzn. czy jeżeli punkty D, E, F leżące
na bokach BC, CA, AB spełniają te równość, to czy musi istnieć punkt P, dla którego
są one rzutami na te boki?
4 mar 19:26
ite:
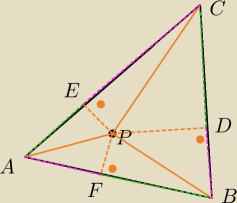
Skorzystaj z tw.Pitagorasa dla ΔAFP, ΔFBP, ΔBPD i pozostałych o w ierzchołku P.
Wylicz z niego najpierw kwadraty długości zielonych odcinków, potem fioletowych.
Porównaj je.
4 mar 19:59
Witcher77: Super udało się

A czy teza działa w drugą stronę ?
4 mar 21:16
wredulus_pospolitus:
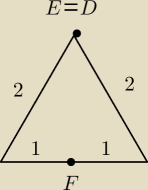
|CD| = 0
|CE| = 0
|BD|
2 + |CE|
2 + |AF|
2 = |DC|
2 + |EA|
2 + |FB|
2
4 + 0 + 1 = 0 + 4 + 1 <−−− spełniony warunek, natomiast nie istnieje taki punkt P WEWNĄTRZ
tego trójkąta, aby E był jego rzutem na bok AC (analogicznie z punktem D)
4 mar 21:22
wredulus_pospolitus:
wniosek

4 mar 21:22
 Skorzystaj z tw.Pitagorasa dla ΔAFP, ΔFBP, ΔBPD i pozostałych o w ierzchołku P.
Wylicz z niego najpierw kwadraty długości zielonych odcinków, potem fioletowych.
Porównaj je.
Skorzystaj z tw.Pitagorasa dla ΔAFP, ΔFBP, ΔBPD i pozostałych o w ierzchołku P.
Wylicz z niego najpierw kwadraty długości zielonych odcinków, potem fioletowych.
Porównaj je.
 A czy teza działa w drugą stronę ?
A czy teza działa w drugą stronę ?
 |CD| = 0
|CE| = 0
|BD|2 + |CE|2 + |AF|2 = |DC|2 + |EA|2 + |FB|2
4 + 0 + 1 = 0 + 4 + 1 <−−− spełniony warunek, natomiast nie istnieje taki punkt P WEWNĄTRZ
tego trójkąta, aby E był jego rzutem na bok AC (analogicznie z punktem D)
|CD| = 0
|CE| = 0
|BD|2 + |CE|2 + |AF|2 = |DC|2 + |EA|2 + |FB|2
4 + 0 + 1 = 0 + 4 + 1 <−−− spełniony warunek, natomiast nie istnieje taki punkt P WEWNĄTRZ
tego trójkąta, aby E był jego rzutem na bok AC (analogicznie z punktem D)
