stereometria Patryk: Hej Wykaż że stosunek objętości stożka do objętości kuli weń wpisanej jest równy stosunkowi pola powierzchni całkowitej stożka do pola powierzchni kuli.

	rH
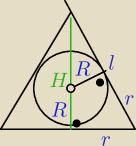
Przyrównując stosunki wyszło mi, że muszę wykazać:		= r+l , r − promień podstawy
	R

stożka, H − wysokośc stożka, l − tworząca stożka, R − promień kuli wpisanej Nie mam pojęcia jak mam to wykazać, trzeba znaleźć jakieś drugie równanie z którego wynika to

	r		H
równanie, które muszę wykazać? Próbowałem z podobieństwa trójkątów		=		ale nie
	R		l−r

da się z nich ułożyć tego równania.

a7:

V1		1/3πr2H
	=
V2		4/3πR3

Pc1		πrl
	=
Pc2		4πR2

	H		l
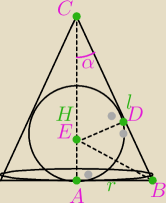
z podobieństwa trójkątów ABC i CDE		=		czyli rH=Rl c.n.w.
	R		r

Jerzy: A od kidy P_c stożka = πrl ?

a7: oj chyba coś przeoczyłam

a7: i w podobienstwie też się pomyliłam

a7: ok teraz dobrze rH=(l+r)R rH=lR+rR rH−rR=lR r(H−R)=lR

H−R		l
	=
R		r

z podobieństwa

H−R		l
	=		cnw
R		r

a7:

	|CE|		|BC|
z podobieństwa		=
	|ED|		|AB|

|CE|=H−R

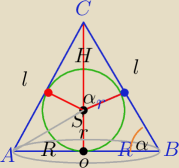Mila: 1) Stosunek objętości:

	1
Vs=		πR2*H
	3

	4πr3
Vk=
	3

	Vs		R2*H
p=		=
	Vk		4r3

2) Stosunek pól powierzchni:

PCS		πR2+πR*l		R2+R*l
	=		=
Pk		4πr2		4r2

	R*(R+l)
q=
	4r2

3)

p		R*H
	=		=1 ponieważ:
q		r*(R+l)

R*H=P_ΔABC

	2R+2l
PΔABC=p*r=		*r=(R+l)*r⇔p=q
	2

Patryk: A dlaczego pole to 1? Nie ma przecież podanych żadnych danych liczbowych

a7: 21:33 r−promień kuli okręgu wpisanego w trójkąt https://matematykaszkolna.pl/strona/542.html

	2P		2P
r=		=
	a+b+c		R+R+l+l

czyli PΔABC=r(R+l) PΔABC równa się również RH

	p		RH		PΔABC
czyli		=		=		=1
	q		r(R+l)		PΔABC

Mila: Patryk masz wszystko rozpisane, czytaj uważnie, ponadto a7 też wyjaśniła. Pole nie jest równe jeden, iloraz ma wartość 1, a to jest różnica .

Eta: R−− dł. promienia kuli r−− dł. promienia stożka l −− dł. tworzącej stożka h −− dł. wysokości stożka

	Vst		r2h		Pst		r(r+l)
L=		=		i P=		=
	Vk		4R3		Pk		4R2

Z podobieństwa trójkątów

r		R
	=		⇒ rh=R(r+l)
l		h−R

	rR(r+l)		r(r+l)
L=		=		=P
	4R3		4R2

L=P

Patryk: Pogubiłem się na chwile, ale już rozumiem. Dziękuję

Eta: