Geomertia analityczna. Imaan: Hejka, mam mały problem z zadaniem z geometrii analitycznej. Treść zadania: Napisz równanie okręgu przechodzącego przez punkt M=(0,1)i stycznego do dwóch prostych o równaniach x+y−2=0 i x+y+3=0 Wyliczyłam promien r= ^5√2₄ i teraz chaiałam zrobic uklad rownań x²+(1−y)²=²⁵₈ oraz odległosci środka od którejś z prostych np.⁵₂=x+y−2 jednak tym sposobem nie wychodzi i chaiałabym wiedzieć co robię nie tak... Zgóry dziękuję za pomoc

Jerzy: A skąd masz takie równanie okręgu ? Przecież M nie jest jego środkiem.

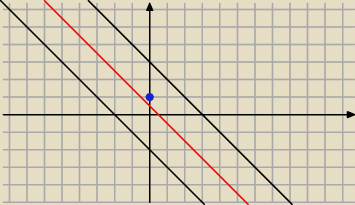
wredulus_pospolitus: A w jaki sposób wyznaczyłaś promień Krok 1. zauważasz, że proste są równoległe Krok 2: wyznaczasz prostą równoległą do tych prostych będąca w połowie odległości tychże prostych Krok 3: punkt M winien leżeć na tej prostej ... a nie leży Sprawdź treść zadania

wredulus_pospolitus: ach faktycznie Jerzy

Imaan: Chwilka.... ale ja tutaj nie mam żadnego równania okręgu, równanie x²+(1−y)²=²⁵₈ to wzór na odległosc punktu M od srodka. Naprowadzcie mnie, proszę

wredulus_pospolitus: tak jak napisałem krok 2: środek okręgu leży na prostej x + y + 1/2 = 0 więc środek okręgu ma współrzędne (a, −a − 0.5)

	25
więc wzór okręgu to (x − a)2 + (y + a + 0.5)2 =
	8

i podstawiasz punkt M w celu wyznaczenia 'a'

Mila: 397292

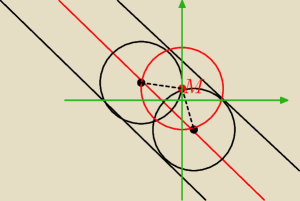
an: Te okręgi mają tak jak wyliczyłeś promień r

	1
środki szukanych okręgów leżą na przecięciu okręgu M o promieniu r z prostą x+y+		=0
	2