okrąg i styczna julik: Napisz równanie okręgu przechodzącego przez punkt M=(0,1) i stycznego do dwóch prostych o równaniach x+y−2=0 i x+y+3=0 Proszę na chłopski rozum. Doszłam do tego, że są równoległe, obliczyłam promień ale nie wiem jak utworzyć drugie równanie.

Leszek: Srodek okregu lezy na prostej miedzy danymi prostymi , czyli wyznaczasz zaleznosc a i b S(a,b) podstawiasz do rownania okregu lacznie z punktem M(0,1) i rozwiazujesz !

julik: właśnie kompletnie nie wiem o co chodzi z tą zależnością ..wiem że ma wyjść równanie z c=1/2 ale nie wiem skąd to się wzięło

Leszek: Promien okregu r = d/2 , d − odleglosc miedzy prostymi , jest na to podany wzor . Prosta na ktorej lezy srodek okregu jest w srodku miedzy danymi prostymi czyli : x+y +0,5 = 0 , czyli b = −a −0,5 ( x −a)² + ( y−b)² = r

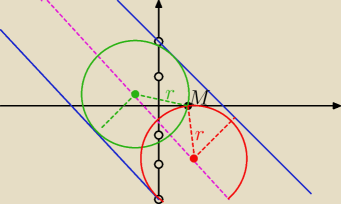
ite: Dodam rysunek pomocniczy do wskazówek Leszka.

Leszek: Wlasnie , dobry rysunek ,ja niestety uzywam komorki , wiec nie robie rysunku , beda dwa rozwiazania dzieki ite:

Jerzy: @Leszek.Nadal czekam na odpowiedzi na dwa pytania,które ci zadałem.

Leszek: Punkt materialny porusza sie tak , ze jego wektor wodzacy okreslony jest wzorem: r= [ 2t+1,3t , t] Wyznaczyc tor punktu i jeo predkosc : predkosc v = [ 2,3,1] jest to wektor o stalym kierunku w przestrzeni , czyli ruch jednostajny prostoliniowy . Tor x= 2t +1 y= 3t z= t /*(−5) x+y −5z −1 = 0 Co to jest plaszyzna , czyli punkt materialny moze znajdowac sie w danej chwili w dowolnym miejscu plaszczyzny , czy jest to tor punktu poruszajacego sie po lini prostej ? ? ?

Jerzy: Czy ty naprawdę nie rozumiesz o co cię pytam ,czy rżniesz g....a ?

Leszek: Sorry ,Jerzy ale tak nie bedziemy prowadzic dialogu ! ! !

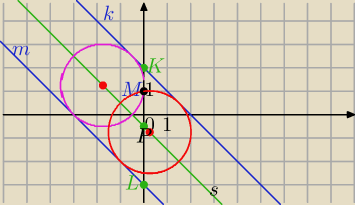
Mila: k: x+y−2=0 ⇔y=−x+2 i m: x+y+3=0⇔ y=−x−3 1) środek odcinka KL K=(0,2) , L=(0,−3)

	1
P=(0,−		)
	2

Środek okręgu lezy na prostej prostej:

	1
s: y=−x−
	2

	1
S=(a, −a−		)
	2

2) Promień okręgu: d− odległość punktu K od prostej m : x+y+3=0

	|0+2+3|		5		5√2
d(K, m)=		=		=
	√12+12		√2		2

	5√2
r=
	4

3) równanie okręgu:

	5√2
(x−a)2+(y−b)2=(		)2 i M∊okręgu
	4

	1		50
a2+(1−(−a−		))2=
	2		16

a²+((3/2)+a)²=(25/8)

	7		1
stąd a=−		lub a=
	4		4

	7		1		5		3
b=		−		=		lub b=−
	4		2		4		4

	7		5		1		3
S1=(−		,		) lub S2=(		,−		)
	4		4		4		4

Równania − napisz sama

ite: pkt M ma współrzędne (0,1) a nie (1,0)

Jerzy: @Leszek,powiedz po prostu „przepraszam,pomyliłem się” i po sprawie,a nie brnij w zaparte.

julik: dziękuję bardzo, udało się !

Mila: Panowie , przenieście się do osobnego wątku Życzę miłej dyskusji

Leszek: Kolego ,Jerzy nie brne w zaparte , Ty natomiast czepiasz sie "slowek" poczytaj podrecznik Analiza Matematyczna prof.K.Maurina to az sie zdziwisz jak sa niektore nazwy matematyczne pozmieniane . w podreczniku K.Witczynski " wybrane zagadnienia z algebry liniowej i geometrii" rownanie prostej w postaci : (x−1)/3 = (y+2)/2 = z/7 jest nazwane rownaniem kierunkowym zas uklad rownan (x−1)/3 = (y+2)/2 i (y+2)/2 = z/7 , nazwane jest rownaniem krawedziowym pek prostych zapisany jest w postaci : α ( 2x+3y +4) +β( 7y +2z +14) =0

Mila: Co Ci się udało julik? Niepotrzebnie pisałam?