Rownanie z parametrem
Karolina: Równanie |−x2+2|x|+5|=2p−4 ma cztery rozwiązania. Wyznacz zbiór możliwych wartości parametru p
. Oblicz sumę kwadratów liczb całkowitych należących do tego zbioru.
Pomocy nie mam pojęcia jak się za to zabrać
8 mar 23:51
wredulus_pospolitus:
1) narysuj f(x) = |−x2 + 2|x| + 5|
2) weź do rącznik linijkę i przesuwaj ją RÓWNOLEGLE do osi OX i sprawdzaj kiedy linijka ma
dokładnie 4 punkty wspólne z funkcją f(x)
3) to są wartości 'm' takie, że 2p − 4 = m .... wyznacz wartości parametru 'p'
8 mar 23:55
Karolina: jak do takiego wzoru narysować wykres
9 mar 00:15
wredulus_pospolitus:
rozdzielić na przypadki
9 mar 00:17
a7:
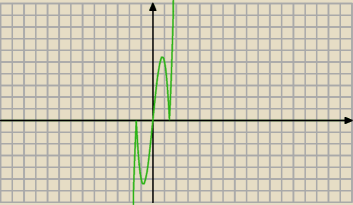
9 mar 00:35
Kasia18: wyszło mi że 4<2p<9 i 2p=10 może ktoś potwierdzić?
9 mar 00:36
a7: wykres z godz 00:35 jest zły
9 mar 00:39
9 mar 00:41
9 mar 00:45
Salazer: 2 zamknięte czy otwarte?
9 mar 00:46
a7: p∊<2,3,4,5>
22+32+42+52=54
9 mar 00:46
Salazer: ja liczyłem i wyszło mi (2,5> m całkowite
9 mar 00:46
a7: zamknięte, gdyż w tych punktach już są te cztery punkty przecięcia
9 mar 00:47
Salazer: mi wyszło że dla 2 są dwa punkty przeciecia a wzwyż juz 4
9 mar 00:48
a7: moim zdaniem dwójka się wlicza (zamknięty nawias) y≥2 i w dwójce jest minimum przez które p
może przejść
9 mar 00:48
a7: poprawka: bez piątki i bez czwórki bo tam się już robi więcej punktów przecięcia
9 mar 00:50
a7: @Salazer, a spojrzałbyś na wykres 00:45, bo może źle odczytuję?
9 mar 00:51
a7: p∊<2,3>
22+32=13
9 mar 01:06
a7: 
9 mar 01:08
Jerzy:
p ∊ (2,5)
32 + 42 = 25
9 mar 10:05

