pies pies: X jest zbiorem całkowitych wartości parametru m dla których równanie |−x²+2|x|+5|=m ma cztery rozwiązania.Oblicz sumę sześcianu liczb należących do zbioru X JAK TO ZROBIC ALGEBRAICZNIE?

pies: kto pomoze pieskowi ...nie chodzi o obliacznie calego tylko w podpunktach jak to zrobic

zombi: Podpowiedź pierwsza. −x²+2|x|+5 = −|x|²+2|x|+5

pies: nie nie napisz w podpunktach prosze bez podpowiddzie

pies: nie rozumimem

Krzysiek: t=|x|

pies: ale napisz w podpunktach

Mila: Algebraicznie . 1) m≥0, m∊C 2) −x²+2|x|+5=m lub −x²+2|x|+5=−m 3) rozwiązujesz w przedziałach (−∞,0), <0,∞) Δ≥0 4) sumujesz liczbę rozwiązań z obu przedziałów, ma być 4. Lepiej to zrobić graficznie. Uprasza się , aby piesek nie szczekał.

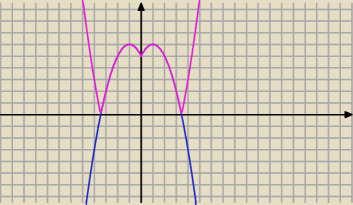
Mila: Metoda graficzna: 1) Rysujesz wykres y=−x²+2x+5 2) Symetria względem OY tej części wykresu , która znajduje się po prawej stronie OY,( pozostałą pomijamy )⇒y=−x²+|x|+5 3) Symetria względem OX tej części wykresu , która leży po osią OX⇒y=|−x²+|x|+5| 4) przesuwasz linijkę od dołu do góry ( tylko różowy wykres Cię interesuje) i odczytujesz dla jakich y przecina wykres w czterech punktach . Odczytuj i sprawdzaj w odpowiedzi wynik.

pies: nie rozumiem bez sensu dlaczego 2) −x2+2|x|+5=m lub −x2+2|x|+5=−m co dalej jak w przedzialach ? to znacczy jak to ze calosc jest w wartosci bezwzg. to jest to /?m≥0, ?

pies: ale to bez sensu 2 ..jak niby mam narysowac wykres y=−x2+2x+5 ? jak bede podstwaial to bedzie to za malo precyzyjne

pies: a nie sczekam juz

Mila: Jak piszesz,że moje rozwiązanie jest bez sensu , to sam rozwiązuj z sensem. m≥0, bo |a|≥0 z definicji dla każdego a ∊R

pies: wiem ze tak jest..ale co to zalatwia cala w.bezwzgledna? ? nie rozumiem ....a nie twoje maja sens wieksze niz moje ...tylko ja sie pytam jak narysowac y=−x2+2x+5

pies: dzieki za pomoc:(

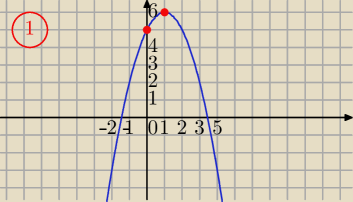
Mila: Szkicujesz wykres; Ważne są w tym zadaniu tylko niektóre dokładne wartości: −x²+2x+5=0 Δ=24 √24=√4*6=2√6

	−2−2√6
x1=		=1+√6≈3.5 nie musi być dokładnie
	−2

lub x₂=1−√6≈−1.5 wystarczy ta dokładność.

	−2
xw=		=1
	−2

y_w=6 W=(1,6) to musi być dokładne f(0)=5 to musi być dokładne Dalej wiesz? Teraz to szkicujesz

pies: dziekuje

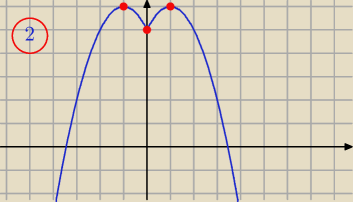
Mila: Naucz się tej metody, bo często trzeba z niej skorzystać. Jak odczytasz , to co trzeba to napisz. Wykres y=−x²+2|x|+5

Eta:

pies: 1 2 3 4 6 to sa odp

Mila: A ty je znalazłeś czy odczytałeś z podręcznika?

pies: nie jednak nie na pewno nie 5 a reszta ..uuuu

pies: to za trudne z rysunku trzeba robic symetrcyczne rysunki jeden na drugim:(

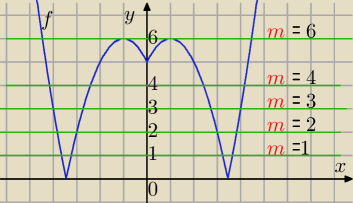
Mila: Dobrze. m=1 lub m=2 lub m=3 lub m=4 lub m=6 X={1,2,3,4,6} Teraz licz sumę sześcianów i gotowe. Patrz na rysunek 21:10, trzeba sobie zrobic taki rysunek, poprzednie leciutko rysujesz ołówkiem, a ostatni kolorem i wszystko widać.

pies: dziekuje milo

pies: A NIE powinny Byc 4 rozwiazania?

Metis: Jest 5 rozwiązań.

pies: ale w pyt ma byc 4

Metis: Pewnie błąd.

pies: X jest zbiorem całkowitych wartości parametru m dla których równanie |−x2+2|x|+5|=m ma cztery rozwiązania.Oblicz sumę sześcianu liczb należących do zbioru X

Metis: Tak, widzimy zadanie. Ale rozwiązanie Mili jest jak najbardziej poprawne.

pies: maja byc 4 rozwiazania

Jerzy: i dla tych pięciu wartości parametru m, są dokładnie cztery rozwiązania

Metis: ... no własnie

pies: dziekuje bardzo