geometria analityczna salamandra: Prosta k przechodzi przez punkt A=(3,2) i przecina dodatnie półosie układu współrzędnych w takich punktach, że iloczyn ich odległości od punktu (0,0) jest równy 25. Wyznacz równanie prostej k. Podpowie ktoś jak ten warunek z iloczynem zapisać?

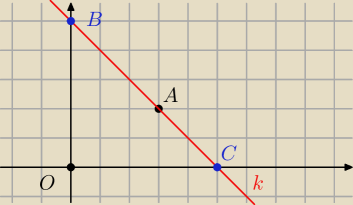
Saizou : B(0, y) oraz C(x,0) zatem |OC|=x |OB|=y |OC|*|OB|=xy xy=25

wredulus_pospolitus: x₀*y₀ = 25 y = ax+b

	25
y0 = b −>		= b
	x0

0 = ax₀ + b 2 = 3a + b układ trzech równań z trzema niewiadomymi. Liczysz

salamandra: coś mi nie wychodzi 0=ax₀+b 2=3a+b

25
	=b
x0

	25
2=3a+
	x0

	25
2−		=3a
	x0

	2		25
a=		−
	3		3x0

	2		25		25
0=(		−		)*x0+
	3		3x0		x0

	2		25		25
0=		x0−		+
	3		3		x0

25		2x0		25
	=		+
3		3		x0

25		2x02		25
	=		+
3		3x0		x0

25		2x02+75
	=		/ * 3
3		3x0

25=2x₀²+75

salamandra: przyznam, że nigdy nie rozwiązywałem układu z trzema niewiadomymi, może złą strategię objąłem

a@b: https://matematykaszkolna.pl/forum/310470.html

salamandra: tego równania odcinkowego to nie znałem

x		y
	+		=1, gdzie x oraz y oznaczają ten punkt który mam podany tak?
a		a

Kiedy stosować ten wzór? Tylko jak mam przecięcie z osiami układu?

wredulus_pospolitus: 25 = xb xa + b = 0 3a + b = 2 x²a + xb = 0 3ax + xb = 2

	25
x2a = −25 −> xa = −
	x

	25		3*25		23		17
3ax = −23 −> −3		= −23 −> x0 =		−> b =		−> a = −
	x		23		3		9

Saizou : prosta k ma równanie y=ax+b A = (3, 2) ∊ k wówczas 2=3a+b b=2−3a y=ax+2−3a (a<0)

	3a−2
funkcja ta przecina oś Y w punkcie B = (0, 2−3a) oraz os X w punkcie C = (		,0)
	a

|OB|*|OC|=25

	3a−2
(2−3a)*		=25
	a

−(3a−2)(3a−2)=25a −9a²+12a−4=25a −9a²−13a−4=0 dokończ

a@b: Dokładnie tak

wredulus_pospolitus: oczywiście źle zrobiłem ... bo '2' nie przemnozyłem przez x

a@b: https://www.matematyczny-swiat.pl/2017/02/rownanie-odcinkowe-prostej.html

salamandra: masakra ile tych zależności trzeba zauważyć i jak wszystko do jednej niewiadomej sprowadzić... myślałem, że to tylko w optymalizacji takie wykręty

salamandra: Już tu właśnie obczaiłem a@b

a@b:

salamandra:

	−4		30
y1=		x+
	9		9

y2=−x+5 dzieki wam!

a@b: Funkcji nie zapisujemy y₁ Odp: prosta k ma równanie y= −x+5 lub y= ...

jc:

	x		y
Równanie prostej przechodzącej przez punkty (a,0), (0,b):		+		=1.
	a		b

ab=25

3		2
	+		=1
a		b

Mnożymy drugie równanie przez a²b=25a. 3*25+2a²=25a Δ=25, a=5 lub a=15/2 b = ...