Pomocy! Krzyś : Prosta k przechodzi przez punkt A(3;2) i przecina dodatnie półosie układu współrzędnych w takich punktach że iloczyn ich odległości od punktu (0;0) wynosi 25. Znajdz równanie prostej k. Mógłny mi to ktoś wytłumaczyć?

ICSP: Zacznij od rysunku.

Jerzy: skorzystaj z równania odcinkowego prostej

Jerzy:

3		2
	+		= 1
a		b

ab = 25

===: Równanie pęku prostych przez punkt A y−2=a(x−3) dla x=0 y=−3a+2

	3a−2
dla y=0 ax=3a−2 ⇒ x=
	a

−(3a−2)²=25a −9a²+12a−4−25a=0 9a²+13a+4=0 Δ=169−144 √Δ=5 a₁=−1 a₂=−4/9 y−2=−(x−3) ⇒ y=−x+5

	4		4		1
lub y−2=−		(x−3) ⇒ y=−		x+3
	9		9		3

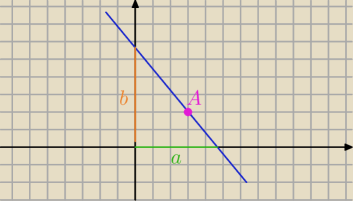
Eta: Jak podał Jerzy Z równania odcinkowego prostej

	x		y
k:		+		=1 A(3,2)∊k i a,b >0
	a		b

3		2
	+		=1 i ab=25
a		b

3b+2a=ab ⇒ 2a=25 −3b i 2ab=50 ⇒ (25−3b)*b=50 3b²−25b+50=0 Δ=25

	10		15
b= 5 i a=5 lub b=		i a=
	3		2

	x		y
k:		+		=1 ⇒ k: x+y−5=0
	5		5

	2x		3y
lub k:		+		=1 ⇒ k: 4x+9y−30=0
	15		10