optymalizacja bryły wz7475: W stożek , którego przekrojem osiowym jest trójkąt równoboczny, wpisano walec o największej objętości. Obliczyć stosunek wysokości h tego walca do promienia R podstawy stożka. Proszę o pomoc, rozwiązałem kilkakrotnie i wychodzi mi wynik √3/3, nie ma takiego wyniku w odpowiedzi.

daras: https://matematykaszkolna.pl/forum/291506.html

daras: sry, zły link wkleiłem https://matematyka.pl/viewtopic.php?t=323789 a potem V'(r) = 0 aπ√3r − 3π√3r² = 0

	a
rπ√3(a − 3r) = 0 ⇔ r = 0 ⋁ r =
	3

	a
czyli Vmax = V(r=		)
	3

	a
promień podstawy stożka R =
	2

	a√3		a√3		a√3		a√3
a wysokość walca h =		− r√3 =		−		=
	2		2		3		6

	h		√3
zatem		=
	R		3

wz7475: dzięki za pomoc, jesteś 4 osobą której wyszedł taki wynik, a nie takiego w odpowiedzi, pewnie tam jest błąd

Mila: A jakie są odpowiedzi do wyboru?

wz7475: √3/4 √3/6 √2/6 √5/6

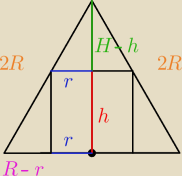
Saizou : Będę piątą osobą, która potwierdzi wynik

H−h		H
	=
r		R

R(H−h)=Hr RH−Rh=Hr Rh=RH−Hr

	RH−Hr
h=		H=R√3
	R

	H(R−r)
h=
	R

h=√3(R−r) V(r, h)=πr²*h V(r)=πr²*√3(R−r)=π√3Rr²−π√3r³ V'(r)=2√3πRr−3π√3r²=0 2Rr−3r²=0

	2
r=0 lub r=		R (sprawdź czy faktycznie w tym punkcie jest max)
	3

	2		√3
h=√3(R−		R)=		R
	3		3

h		√3   R 3		√3
	=		=
R		R		3