Stereometria Hej: W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem α. Przez krawędź podstawy o długości a poprowadzono płaszczyznę tworzącą z płaszczyzną podstawy kąt β (0<β<α). Oblicz pole otrzymanego przekroju. Może ktoś pomóc i wytłumaczyć to zadanie? Stereometria zawsze była moją piętą achillesową w matematyce.

a7: https://matematykaszkolna.pl/forum/242781.html

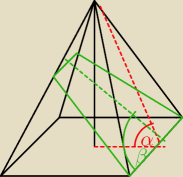
salamandra: coś więcej powiedziano o tej plaszczyźnie?

Hej: Nie, podałem całe polecenie

salamandra: Bo zastanawiałem się, czy ta płaszczyzna nie może być trojktem

a7: w linku jest rozwiązanie

a7: tutaj też https://zadania.info/d171/3145173

Hej: Widzę i no cóż to jest ciekawe zadanie, dziękuję

salamandra: A dlaczego ta płaszczyzna nie może być trójkątem?

a7: bo β<α

salamandra: A wierzchołek nie mógłby być tak jakby pośrodku ściany bocznej?

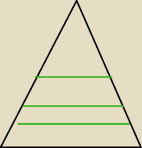
a7: tam zawsze będzie (u góry mniejsza lub większa "kreska")

a7: bo przekrój jest częścią całej płaszczyzny i przechodzi przez cały trójkąt w poprzek

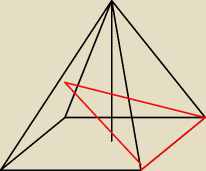
salamandra: Ja to widziałem tak na przykład

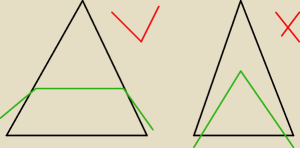
a7: ja narysowałam tę ścianę boczną gdzie przekrój przechodzi jako prosta a nie jako wierzchołek trójkąta wtedy to nie byłby przekrój tylko trójkąt dotykający płaszczyzny czwartej ściany bocznej

salamandra: przekrój, czyli po prostu kroimy po ścianie? W cudzysłowie "nie wycinamy wzorków"?

a7: no tak, jakbyś nożem tort kroił pod kątem