Przekrój ostrosłupa.
jakubs:
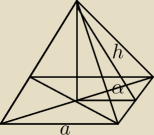
Zadanko ze zbioru A. Kiełbasy nr 531
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod
kątem α. Przez krawędź boczną o długości a poprowadzono płaszczyznę tworzącą z płaszczyzną
podstawy kąt β ()<β<α). Oblicz pole otrzymanego przekroju.
20 mar 13:22
jakubs:
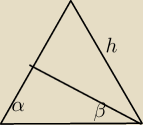
Ten przekrój to trapez równoramienny. Ale nie mam pomysłu jak ruszyć to zadanie

Jakaś wskazówka ?
20 mar 13:24
...:
1. zamieszczasz zadanie ... to przepisz (przerysuj) je dokładnie.
Po co marnotrawisz czas innych na twoje zgaduj−zgadule ...
20 mar 13:38
jakubs: Przepisałem treść dokładnie. Rysunek dałem swój, bo chcę tylko wskazówkę, a nie zeby mi je ktoś
rozwiązał...
Gdzie masz "zgaduj−zgadule" ?
20 mar 13:39
jakubs: W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod
kątem α. Przez krawędź boczną o długości a poprowadzono płaszczyznę tworzącą z płaszczyzną
podstawy kąt β (0<β<α). Oblicz pole otrzymanego przekroju.
20 mar 13:40
...:
... przepisujesz drugi raz i znów "wklejasz" głupawkę.
przez krawędź postawy a nie przez
krawędź boczną 
20 mar 13:43
jakubs: Masz racje.
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod
kątem α. Przez krawędź podstawy o długości a poprowadzono płaszczyznę tworzącą z płaszczyzną
podstawy kąt β (0<β<α). Oblicz pole otrzymanego przekroju.
20 mar 13:45
Mila:
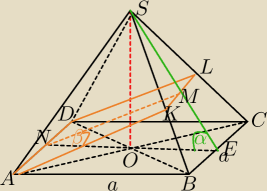
20 mar 17:04
jakubs: Mila dzięki za rysunek. Jak wyznaczyć |KL| ?
Z podobieństwa trójkątów jakoś by się dało ?
20 mar 17:42
Mila:
Np. obliczasz kolejno
1) SE
2)ME
3)SM
4) ΔSKL∼ΔBCE
20 mar 17:44
jakubs: Poddaje się z tym zadaniem, za głupi na to jestem.
20 mar 18:15
Mila:
Co obliczyłeś?
20 mar 18:25
20 mar 18:28
Mila:
1) W ΔSOE:
|SE|*cosα=0,5a
2) W ΔNEM: z tw. sinusów
| NM | | a | |
| = |
| |
| sinα | | sin(180−(α+β)) | |
| | asinα | |
|NM|=htrapezu= |
| |
| | sin(α+β) | |
| ME | | a | | asinβ | |
| = |
| ⇔|ME|= |
| |
| sinβ | | sin(α+β) | | sin(α+β) | |
3)
|SM|=|SE|−|ME|
| | a | | asinβ | | sin(α+β)−2sinβcosα | |
|SM|= |
| − |
| =a* |
| |
| | 2cosα | | sin(α+β) | | 2 cosα*sin(α+β) | |
|KL|=|SM|*2cosα
Podstawiaj i licz dalej
20 mar 19:05
jakubs: Mila dzięki serdeczne !
Doszedłem do tego
| | [a*sin(α+β)+sin(α+β)−2sinβcosα]*a*sinα | |
Pt= |
| |
| | 2sin2(α+β) | |
Próbuje coś wyciągnąć przed nawias, ale nic sensownego z tego mi nie wychodzi.
20 mar 19:26
Mila:
Mała pomyłeczka .
bez tego a w pierwszym składniku licznika , poza nawiasem wtedy a2*sin α.
Potem rozpisz sin(α+β)=...
20 mar 19:36
jakubs: | | a[sin(α+β)−2sinβcosα] | |
|KL|= |
| |
| | sin(α+β) | |
| | | a*sin(α+β)+a[sin(α+β)−2sinβcosα] | |
| | | sin(α+β) | |
| | a*sina | |
Pt= |
| * |
| |
| | 2 | | sin(α+β) | |
| | a*sina[a*sin(α+β)+a[sin(α+β)−2sinβcosα]] | |
Pt= |
| |
| | 2sin2α | |
| | a2sinα[2sin(α+β)−2sinβcosα] | |
Pt= |
| |
| | 2sin2α | |
Jest ok?
20 mar 20:09
Mila: Nie. Problem z ułamkami.
| | a*sin(α+β)+a*[sin(α+β)−2sinβcosα] | | a*sinα | |
Pt= |
| * |
| = |
| | 2sin(α+b) | | sin(α+β) | |
| | 2sin(α+β)−2sinβ*cosα | |
=a2*sinα* |
| = |
| | 2sin2(α+β) | |
| | 2*sinα*cosβ+2sinβcosα−2sinβ*cosα | |
=a2sinα* |
| = |
| | 2sin2(α+β) | |
| | a2*sinα*sinα*cosβ | |
= |
| |
| | sin2(α+β) | |
⇔
| | a2*sin2α*cosβ | |
Ptrapezu= |
| |
| | sin2(α+β) | |
20 mar 20:22
jakubs: Jejku wpisywałem w mianowniku 2sin
2α, a na kartce mam 2sin
2(α+β). Wcześniej zgubiłem a w
|KL| i dlatego źle miałem obliczenia.
Dziękuje serdecznie za pomoc


20 mar 20:29
Mila:

20 mar 20:30
 Zadanko ze zbioru A. Kiełbasy nr 531
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod
kątem α. Przez krawędź boczną o długości a poprowadzono płaszczyznę tworzącą z płaszczyzną
podstawy kąt β ()<β<α). Oblicz pole otrzymanego przekroju.
Zadanko ze zbioru A. Kiełbasy nr 531
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod
kątem α. Przez krawędź boczną o długości a poprowadzono płaszczyznę tworzącą z płaszczyzną
podstawy kąt β ()<β<α). Oblicz pole otrzymanego przekroju.
 Ten przekrój to trapez równoramienny. Ale nie mam pomysłu jak ruszyć to zadanie
Ten przekrój to trapez równoramienny. Ale nie mam pomysłu jak ruszyć to zadanie  Jakaś wskazówka ?
Jakaś wskazówka ?




