stereometria
salamandra:
Zadanie:
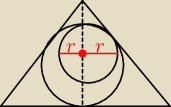
Kula wpisana w stożek ma promień 2 a kula styczna do kuli wpisanej i powierzchni bocznej stożka
ma promień długości 1. Środki obu kul leżą na wysokości stożka. Oblicz objętość i pole
powierzchni całkowitej tego stozka.
Dobry mniej więcej rysunek szkicowy? Jako że ciezko mi sobie wyobrazić to że ta druga kula ma
wspólny środek oraz jest styczna jeszcze do powierzchni bocznej
2 mar 17:44
a7:
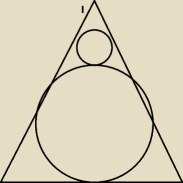
?
2 mar 17:52
Saizou :
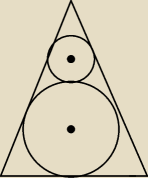
Taki bałwanek powstanie

2 mar 17:53
salamandra: no tak

Dzięki
2 mar 17:53
salamandra: Źle doczytałem− myślałem że ma być WSPÓLNY środek

2 mar 17:54
salamandra: W ogóle też wam forum wolno chodzi?
2 mar 17:55
a7: tak (wolno chodzi)
2 mar 17:56
Saizou : Tak, wczoraj też był z tym problem. Chyba za dużo maturzystów się obudziło przed majem

2 mar 17:56
salamandra: Domyślam się, że muszę tutaj jakoś z podobieństwa kombinowac?
2 mar 17:57
Saizou :
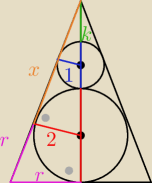
2k+2=k+4
k=2
Wysokość stożka H=4+2+2=8
Pomarańczowy odcinek z Pitagorasa
x
2+4=36
x
2=32
x=4
√2
r też z Pitagorasa
(r+4
√2)
2=r
2+64
r
2+8
√2r+32=r
2+64
8
√2r=32
r=2
√2
tworząca stożka r+x=6
√2
reszta do doliczenia

2 mar 18:27
salamandra: Sam jedynie zdołałem k i wysokość, dalej brakowało pomysłu, dzięki

2 mar 18:41
salamandra: Sam jedynie zdołałem k i wysokość, dalej brakowało pomysłu, dzięki

2 mar 18:42
Saizou :
Twierdzenie Pitagorasa zawsze pomaga

2 mar 18:43
salamandra: l=6
√2
Pp=(2
√2)
2*π= 8π
Pb=π*2
√2*6
√2=24π
Pc=32π
?
2 mar 18:58
Saizou :

2 mar 19:00
2 mar 19:08
 Zadanie:
Kula wpisana w stożek ma promień 2 a kula styczna do kuli wpisanej i powierzchni bocznej stożka
ma promień długości 1. Środki obu kul leżą na wysokości stożka. Oblicz objętość i pole
powierzchni całkowitej tego stozka.
Dobry mniej więcej rysunek szkicowy? Jako że ciezko mi sobie wyobrazić to że ta druga kula ma
wspólny środek oraz jest styczna jeszcze do powierzchni bocznej
Zadanie:
Kula wpisana w stożek ma promień 2 a kula styczna do kuli wpisanej i powierzchni bocznej stożka
ma promień długości 1. Środki obu kul leżą na wysokości stożka. Oblicz objętość i pole
powierzchni całkowitej tego stozka.
Dobry mniej więcej rysunek szkicowy? Jako że ciezko mi sobie wyobrazić to że ta druga kula ma
wspólny środek oraz jest styczna jeszcze do powierzchni bocznej
 ?
?
 Taki bałwanek powstanie
Taki bałwanek powstanie 
 Dzięki
Dzięki








 jakby Twoje sokole oko chciało na te wypociny spojrzeć, byłbym wdzięczny https://matematykaszkolna.pl/forum/397747.html
jakby Twoje sokole oko chciało na te wypociny spojrzeć, byłbym wdzięczny https://matematykaszkolna.pl/forum/397747.html