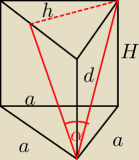
stereometria salamandra: W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równe jest sumie pól obu podstaw. Oblicz cosinus kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej. 2Pp=Pb

a2√3
	=2Pp
2

Pb=3*a*H=3aH

	a2√3
3aH=		/ * 2
	2

6aH=a²√3

	a2√3		a√3
H=		=
	6a		6

	a√3
(		)2+a2=d2
	6

3a2
	+a2=d2
36

a2
	+a2=d2
12

13a2
	=d2
12

	a√39
d=
	6

	a√3
h=
	2

	a√3   2		a√3		6		3√3		3√117
sinα=		=		*		=		=		=
	a√39   6		2		a√39		√39		39

	√117		3√13
		=
	13		13

	3√13
(		)2+cos2α=1
	13

117
	+cos2α=1
169

	52
cos2α=
	169

	52		2√13
cosα=√		=
	169		13

Jest ok czy można krócej?

a7: w linku godz.18:37 zrobione jakby ciut krócej przez dero2005 https://matematykaszkolna.pl/forum/32864.html

a7: ale tam w linku jest pominięte kilka obliczeń szczegółowych i może stąd się wydaje, że jest krócej...

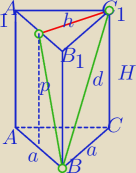Mila: Nie wiem , czy krócej, ale inaczej 1)

a2√3		a2√3
	*2=Pb⇔		=3*a*H⇔
4		2

	a√3
H=
	6

======

	a√3
2) d2=a2+H2⇔d2=a2+(		)2⇔
	6

	13
d2=		a2
	12

	a√3		a
p2=(		)2+(		)2
	6		2

	1
p2=		a2
	3

cosα>0

	p
cos2α=
	d

	1   a2 3		4
cos2α=		=
	13   a^^2 12		13

	2
cosα=
	√13

=============

salamandra:

Mila: tam jest błąd :

	p2
cos2α=
	d2

Pewnie zauważyłeś?

salamandra: Przyznam, że nie, jesteś tutaj takim autorytetem, że to grzech doszukiwać się u Ciebie błędów