zadanie dla odważnych
Visu: W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej jest równe sumie pól obu
podstaw. Oblicz kosinus kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany
bocznej.
Jeśli ktoś moze ^^ prosze o pomoc
6 sty 15:57
...:::BENIO/̵͇̿̿/'̿'̿̿̿ ̿̿̿̿ :
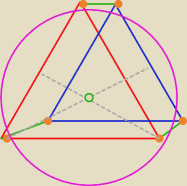
okrąg opisany na trójkąt ...:::∑αℛ⊂i∩:::...
6 sty 17:15
...:::BENIO/̵͇̿̿/'̿'̿̿̿ ̿̿̿̿ : pomyłka
6 sty 17:17
Visu: hmm nie mam niektórych znaczków ale obliczen nie ma?
narysowac to jeszcze latwo jest
6 sty 18:03
Godzio: zaraz coś pokombinuje
6 sty 18:06
Godzio:
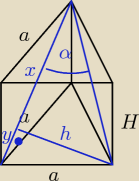
| | a2√3 | | a2√3 | |
3*aH = 2* |
| = |
|
|
| | 4 | | 2 | |
a
2√3 = 6aH
a
√3=6H
a=3
√3H
d
2 =a
2 + H
2
d
2 = 27H
2 + H
2
d=2
√7H
x+y = d => y = d−x
y
2 + h
2 = a
2 => h
2 = a
2−y
2
x
2 + h
2 = d
2 => x
2 +a
2−y
2 = 28H
2
x
2 + 27H
2 −(d−x)
2 = 28H
2
x
2 −(d
2 − 2x +x
2) = H
2
x
2 −(28H
2 − 2dx + x
2) = H
2
x
2 −28H
2 + 4
√7Hx −x
2 = H
2
4
√7Hx = 29H
2
| | x | | 29√7H | | 1 | | 29 | |
cosα= |
| = |
| * |
| = |
|
|
| | d | | 28 | | 2√7H | | 56 | |
Mam nadzieje ze sie ni pomyliłem
6 sty 18:19
Visu: woow
hmm to sama sobie wytlumaczyc spróbuje
Chcesz wiecej takichzadanek?
6 sty 18:33
Godzio: a mozesz dać
6 sty 18:35
Eta:
Godzio ..... pomyłka:
a
√3= 6H => a =
2√3*H => a
2 = 12H
2
to d
2= 12H
2 + H
2 = 13H
2
teraz najprościej ze wzoru cosinusów
| | d2 +d2 −a2 | | 26H2 − 12H2 | | 14 | | 7 | |
cos α= |
| = |
| = |
| = |
|
|
| | 2*d*d | | 2*13H2 | | 26 | | 13 | |
odp:
cos α= 713
6 sty 18:53
Visu: a x i y niepotrzebnie wyliczane
6 sty 18:58
Eta:
Napisałam ....... najprościej ze wzoru cosinusów !
i to wszystko (bo mniej obliczeń
6 sty 19:12
Visu: thx u all
6 sty 19:13
Wodzirej: Złe rozwiązanie, w zadaniu jest mowa o kącie nachylenia do drugiej ściany bocznej a nie do
przekątnej drugiej ściany bocznej, więc drugie ramię kąta powinno być poprowadzone do środka
krawędzi a. Sam się na tym jebnąłem.
19 lut 18:02
dero2005:
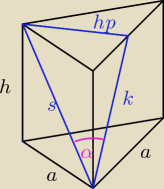
k =
√h2 + (a2)2 = a
√3
19 lut 18:37
nicoll: a skąd w Pb=2PP= 3a*h ? skad to się wzieło to 3a*h
5 mar 21:13
Halucynacja Hemoglobina: stąd , że Pb = 3 * a*h −−−> masz tu trzy prostokąty o wymiarach a i h
6 mar 20:52
ja: jakim cudem h
2 +(a/2)
2 = k
2 z tego wychodzi k= a
√3 mi wychodzi jeszcze dzielone na 3
18 mar 17:57
Kindzia: Zgadza się, k powinno byc (a √3)/3.
29 mar 12:32
vangur: Czy mógłby ktoś policzyć to s = √a2 + h2?
Bo nie mogę tego za chiny policzyć.
22 paź 20:27
dero2005:
s =
√a2 + h2 =
√a2 + (a√36)2 =
√a2 + 3a236 =
=
√a2 + a212 =
√12a2+a212 =
√13a212 =
| | √13 | | √13 | | √3 | | √39 | |
= a |
| = a |
| * |
| = a |
| |
| | √12 | | 2√3 | | √3 | | 6 | |
22 paź 21:42
Mati: Nie można było tak od razu?
10 mar 20:15
Marta: Skąd ta prosta k ? Skąd to wiadomo ? DLACZEGO TAK ?
26 kwi 21:30
diss: JD
25 maj 23:26
Poprostupatryk: Ja to zrobiłem, jeszcze fajniej. Za kąt między przekątnymi sąsiadujących ścian bocznych dałem
2α.
Poprowadziłem wysokość z wierzchołka na którym zbudowane jest 2α. I policzyłem sinusa,
pitagoras.
| | 7 | |
cos2α=1−sin2α. Wyszło |
| . |
| | 13 | |
Eta zrobiła chyba najszybciej. No ale warto poznawać różne rozwiązania
26 maj 00:19
Eta:
26 maj 00:28
Oliwia: A ile w tym zadaniu sinus wyszedł i jak to policzyć
1 maj 07:44