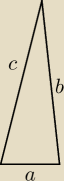
geometria MalWas: Liczby a, b, c spełniające warunek 2a<b+c są długościami boków trójkąta. Czy kąt leżący naprzeciw boku a ma miarę większą czy mniejszą niż 60 stopni?

a7: mniejszą

MalWas: a7 a jak to jakoś udowodnić? zapisać?

a7: niestety przyszedł mi do głowy tylko taki prosty przypadek na szybko, bo myślałam że to zwykłe pytanie np. z testu ale zaraz się zastanowię, poszukam

wredulus_pospolitus:

	b+c
a <
	2

z tw. cosinusów:

	b+c		1
a2 = b2 + c2 − 2bc*cosα < (		)2 =		(b2 + c2 + 2bc)
	2		4

więc otrzymujemy: 3b² + 3c² − 8bccosα − 2bc < 0 3(b − c)² + 4bc − 8bc*cosα < 0 3(b − c)² + 4bc*(1 − 2cosα) < 0 −> na pewno musi zachodzić: cosα > 0.5 Argumentacja ... tylko dla cosα > 0.5 może zajść 4bc(1 − 2cosα) < 0 więc tylko wtedy lewa strona ma jakąkolwiek szansę być ujemna

Adamm:

	b2+c2−a2		b2+c2−(c+b)2/4
a2 = b2−2bc*cosα+c2 ⇒ cos α =		>		=
	2bc		2cb

	2b2+2c2+(b−c)2
=		≥ 1/2
	8bc

a7: https://matematykaszkolna.pl/strona/406.html cosα>1/2 dla α<60^o

MalWas: Dziękuję bardzo

wredulus_pospolitus: Wow ... powrót po 15 dniach

MalWas: Nadal i wciąż to zadanie nie daje mi spokoju. Pewnych etapów chyba jednak nie rozumiem. Mógłby mi to ktoś wytłumaczyć? Korzystam z tw. cosinusów. Utknęłam przy szacowaniu. Dlaczego tam jest (c+b)²/4

wredulus_pospolitus: 2a < b + c <−−− nierówność trójkąta została zastosowana czyli:

	b+c
a <
	2

	b+c
a2 < (		)2
	2

więc:

	b+c
b2 + c2 − 2bc*cosα < (		)2
	2

MalWas: aaa... jejciu... jak blondynka... hahahahaha

MalWas: Czy tam nie powinno być 3b²+3c²−2bc / 8bc ?

wredulus_pospolitus: "tam" znaczy gdzie

MalWas: ^{b2 + c2 − (b+c)2 / 4} _2bc = ^{4b2+4c2−b2−2bc−c2/4}_2bc = ^{3b2+3c2−2bc}_8bc ≥1/2

MalWas: To jest poprawnie?

wredulus_pospolitus: patrz co napisał Adamm o 21:14 i porównaj ze swoimi zapiskami

wredulus_pospolitus: staraj się też zapisywać ułamki za pomocą funkcji U a nie u:

1
	a nie 1(√2)3 chyba nie muszę mówić co jest bardziej czytelne
(√2)3

MalWas: To co napisał Adamm jest poprawnie?

MalWas: OK. No właśnie się zastanawiałam czemu moje ułamki są takie brzydkie.

wredulus_pospolitus: tak ... jest poprawne tylko nie wiem czy rozumiesz dlaczego ten ułamek jest nie mniejszy niż 1/2

MalWas: Drogi kolego, bądź tak uprzejmy i mi napisz.

wredulus_pospolitus:

2b2 +2c2 + (b−c)2		2b2+2c2
	≥		(bo (b−c)2 ≥ 0)
8bc		8bc

2b2+2c2		b2 + c2		b2 − 2bc + c2 +2bc
	=		=		=
8bc		4bc		4bc

	(b−c)2 + 2bc		2bc
=		≥		(z tego samego powodu co wcześniej)
	4bc		4bc

2bc		1
	=
4bc		2

koooniec

MalWas: Bardzo Ci dziękuję. Jesteś wielki! <3

wredulus_pospolitus: raptem 180cm −−− taki wielki to ja nie jestem