stereometria
salamandra:
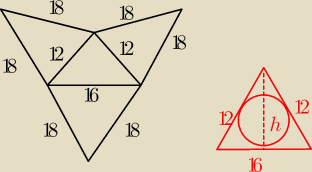
Na rysunku przedstawiono siatkę bryły. Nazwij tę bryłę. Oblicz pole powierzchni całkowitej oraz
objętość V
8
2+h
2=12
2
h=4
√5
Spodek wysokości będzie padał na środek okręgu opisanego/wpisanego w ten trójkąt.
Na ścianie bocznej prowadzę wysokość h
b
ściana boczna to trójkąt równoramienny o bokach 16,18,18
więc 8
2+h
b2=18
2
h
b=2
√65
(2
√65)
2=r
2+H
2
Czemu mi z tego nie wychodzi poprawnie?
24 lut 19:42
wredulus_pospolitus:
Bo wysokość tego czworościanu NIE JEST w środku okręgu wpisanego w podstawę
Gdyby tak było to mamy:
h
'dolnej' ściany = 2
√92 − 42 = 2
√65
h
podstawy = 4
√32 − 22 = 4
√5
d −−− krawędź ściany = 18
więc masz:
| | 2hpodstawy | |
(1) hczworościanu2 + ( |
| )2 = 182 |
| | 3 | |
| | hpodstawy | |
(2) hczworościanu2 + ( |
| )2 = (2√65)2 |
| | 3 | |
podstawiamy
| | 320 | | 2596 | |
(1) hczworościanu2 = 324 − |
| = |
| |
| | 9 | | 9 | |
| | 80 | | 2260 | |
(2) hczworościanu2 = 260 − |
| = |
| |
| | 9 | | 9 | |
sprzeczność

24 lut 19:56
salamandra: | | abc | |
Wyszło mi ostatecznie obliczając R= |
| i z tw. Pitagorasa R2+H2=182 |
| | 4PΔ | |
Domyślam się, że zadziałałoby to tylko w wypadku, gdy byłby to trójkąt równoboczny? Właśnie do
identycznej sprzeczności doszedłem....
A dlaczego trzeba skorzystać akurat z okręgu opisanego a nie wpisanego? Co gdybym policzył r ze
| | PΔ | |
wzoru |
| , gdzie p= połowa obwodu i wtedy zrobił |
| | p | |
r
2+H
2=h
b2?
24 lut 20:00
wredulus_pospolitus:
Okrąg opisany na trójkącie daje Ci punkt (środek okręgu) równo odległy do wierzchołków
podstawy.
Jako, że krawędzie boczne są sobie równe to otrzymujesz takie same (trzy) trójkąty prostokątne
o podstawa: R, hczworościanu, krawędź boczna
Dlatego więc środek okręgu opisanego na podstawie (w tym przypadku −−− ze względu na krawędzie
boczne) prezentuje nam gdzie znajduje się wierzchołek tegoż czworościanu.
24 lut 20:04
wredulus_pospolitus:
Natomiast zauważ, że w trójkącie równobocznym (i tylko wtedy) środek okręgu opisanego i
wpisanego leży dokładnie w tym samym punkcie.
24 lut 20:05
wredulus_pospolitus:
gdyby krawędzie boczne NIE BYŁY by sobie równe, to wierzchołek tego czworościanu nie
znajdowałby się nad środkiem okręgu opisanego na podstawie (jego położenie zależne byłoby od
długości krawędzi bocznych).
24 lut 20:07
salamandra: To jak wtedy sobie poradzić? Bo idąc tym sposobem, znowu doszłaby sprzeczność prawda? Bo te
wysokości mogłyby być nachylone pod różnym kątem do którejś z krawędzi bocznych, a raczej
krawędzie boczne do niej i gdyby krawędzie boczne nie były równe, to mogłyby być różne
wysokości?
24 lut 20:14
wredulus_pospolitus:
Jeżeli wierzchołek nie znajduje się ponad środkiem okręgu opisanego na podstawie ... wtedy
będzie podane gdzie się on znajduje (ponad którymś wierzchołkiem bądź ponad którąś krawędzią
podstawy) ... nie sądzę aby znalazło się zadanie w którym masz bliżej nieokreślone miejsce
wierzchołka i musisz wyznaczyć miejsce jego rzutu na płaszczyznę podstawy.
24 lut 20:17
salamandra: Czyli generalnie wpoić sobie, ze będzie to środek okręgu OPISANEGO, a nie wpisanego i tyle?
24 lut 20:18
wredulus_pospolitus:
opisanego będzie jeżeli krawędzie boczne są sobie równe, jeżeli nie są równe to w zadaniu winno
być podane gdzie leży rzut wierzchołka na płaszczyznę
24 lut 20:24
wredulus_pospolitus:
Ale na pewno −−− należy zapomnieć, że wyznaczasz z okręgu wpisanego
24 lut 20:25
salamandra: Dzięki

24 lut 20:26
salamandra:
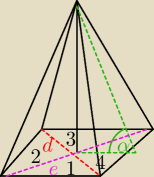
teraz mam zadanie:
podstawą ostrosłupa jest romb, którego bok ma długość a, a krótsza przekątna ma długość d.
Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt α. Wyraź objętość tego ostrosłupa w
zależności od a,d i funkcji trygonometrycznej kąta α.
(0,5e)
2+(0,5d)
2=a
2
e
2=4a
2−d
2
e=
√4a2−d2
| | 1 | | 1 | | 1 | | 1 | |
P1=P2= |
| * |
| *√4a2−d2* |
| *d*sin90 = |
| d√4a2−d2 |
| | 2 | | 2 | | 2 | | 8 | |
P3=P4=P1=P2
| | 1 | | 1 | | 1 | | 1 | |
V= |
| * |
| *d√4a2−d2*tgα* |
| a= |
| a*d√4a2−d2*tgα |
| | 3 | | 2 | | 2 | | 12 | |
No i nie wychodzi jak powinno...
24 lut 20:38
Mila:
Spodek wysokości ostrosłupa.
1)
Jeżeli krawędzie boczne ostrosłupa są nachylone do podstawy pod takim samym kątem do
płaszczyzny podstawy , to spodek wysokości ostrosłupa leży w środku okręgu opisanego na
podstawie.
2)
Jeżeli krawędzie boczne ostrosłupa są tej samej długości , to spodek wysokosci ostrosłupa
leży w środku okręgu opisanego na podstawie.
3)
Jeżeli ściany boczne ostrosłupa są nachylone do podstawy pod takim samym kątem, to spodek
wysokości ostrosłupa leży w środku okręgu wpisanego w podstawę.
24 lut 20:40
salamandra: 
24 lut 20:42
wredulus_pospolitus:
Po co liczysz P
1, P
2, itd.

| | d*e | |
Prombu = |
| <−−− koniec ... podstawiasz i masz |
| | 2 | |
24 lut 20:43
salamandra: debil... no debil....

wiedziałem że jest wzór e*f*0,5*sinα, ale przecież α=90, a ja
sobie wpoiłem, że nie znam kąta więc z tego nie skorzystam...
24 lut 20:44
wredulus_pospolitus:
Miluś −−− jeszcze można dodać:
4)
Jeżeli wysokości wszystkich ścian bocznych są tej samej długości to spodek wysokości ostrosłupa
lezy w środku okręgu wpisanego w podstawę.
24 lut 20:45
wredulus_pospolitus:
A jak 'powinno' wyjść

24 lut 20:46
salamandra: | | d2*(4a2−d2)*tgα | |
V= |
| , gdzie d∊(0;2a) i α∊(0;90) |
| | 24a | |
24 lut 20:47
salamandra: | | d*√4a2−d2*tgα*a | |
Mój wynik: V= |
| |
| | 12 | |
24 lut 20:47
wredulus_pospolitus:
ach ... już wiem gdzie jest błąd
24 lut 20:47
salamandra: No nie gadaj, że spodek wysokości nie będzie na środku rombu....
24 lut 20:49
Mila:
Dzięki
Arturku, dopiszę następnym razem
 salamndra
salamndra , piszę rozwiązanie, tymczasem narysuj na kartce romb i wpisz w niego okrąg.
24 lut 20:49
salamandra: cóż.... n−ta z rzędu nieprzespana noc się szykuje....
24 lut 20:50
wredulus_pospolitus:
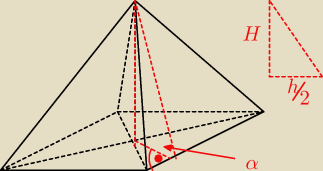
to co zaznaczyłeś to NIE JEST kąt α
24 lut 20:51
salamandra: no tak, bo to nie jest trójkąt równoramienny/równoboczny......
24 lut 20:52
wredulus_pospolitus:
będzie w środku rombu, ale kąt który zaznaczyłeś nie jest kątem pomiędzy ścianą boczną a
podstawą
To co zaznaczyłeś będzie tylko jeżeli ten romb jest kwadratem

| | H | |
winno być tgα = |
| |
| | 0.5hpodstawy | |
24 lut 20:53
salamandra: no tak, tylko jak teraz wyznaczyc h podstawy− przyrównać dwa wzory na pole?
24 lut 20:55
wredulus_pospolitus:
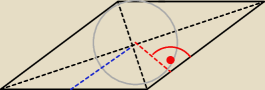 czerwona
czerwona linia to bok (na podstawie) szukanego trójkąta (czyli h/2), a nie
niebieska
(czyli a/2)
24 lut 20:56
wredulus_pospolitus:
Tak ... to jest jeden ze sposobów (porównanie wzorów na pole rombu)
24 lut 20:57
wredulus_pospolitus:
Zauważ, że to jest przykład ostrosłupa gdzie kąty nachylenia ścian bocznych (ale i także
wysokości tychże ścian bocznych) są sobie równe ... dlatego środek okręgu wpisanego.
Inaczej poczyniona argumentacja pozwoli stwierdzić, że będzie to przecięcie się przekątnych
(czyli ten sam punkt).
Mam nadzieję, że z rysunku 20:56 rozumiesz jaki błąd popełniłeś
24 lut 21:01
salamandra: Taaak, właśnie chciałem powiedzieć, ze niepotrzebnie mi na tyle sposobów to tłumaczysz

po
pierwszym rysunku już wiedziałem
24 lut 21:03
salamandra: Jednak ciężko mi sobie wyobrazić, że tam już nie moge być kąt α, bo jakby, weźmy trojkat,
pochylmy go w stosunku do biurka, no to w każdym miejscu na ścianie jest identyczny kat, czy
to co napisałeś wynika stricte z definicji kata dwusciennego?
24 lut 21:15
Mila:
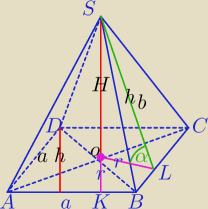
|DB|=d
1) w ΔAOD:
|AC|=
√4a2−d2
3) W ΔSOL:
| | d*√4a2−d2 | |
H=r*tgα= |
| *tgα |
| | 4a | |
| | 1 | | 1 | | d*√4a2−d2 | |
4) V= |
| * |
| *d*√4a2−d2* |
| *tgα |
| | 3 | | 2 | | 4a | |
========================
24 lut 21:17
wredulus_pospolitus:
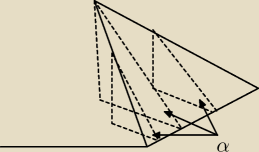
to jest kąt nachylenia ściany bocznej do podstawy
zauważ, że te wszystkie odcinki na ścianie bocznej są PROSTOPADŁE do krawędzi podstawy.
Wyobraź sobie że mamy tą ścianę boczną i ją 'obniżamy (zmniejszamy wysokość ostrosłupa) ...
cały czas te odcinki na ścianie bocznej są prostopadłe do krawędzi podstawy podstawy.
W końcu h{

strosłupa] = 0 ... cały czas te odcinki są prostopadłe do podstawy ... czyli ten
środkowy odcinek to nic innego jak wysokość trójkąta wyznaczonego przez podstawę i połowy
przekątnych −−− czyli połowa wysokość rombu
24 lut 21:24
wredulus_pospolitus:
zauważ, że ściana boczna NIE JEST trójkątem równoramiennym ... więc wysokość tego trójkąta
(ściany bocznej) nie będzie spadać w połowie podstawy

24 lut 21:26
salamandra: No wiem, tylko nie rozumiem czemu ten odcinek łączący spodek wysokości z punktem na krawędzi
podstawy musi tworzyć kat prosty
24 lut 21:29
wredulus_pospolitus:
ponieważ jest on RZUTEM wysokości ściany bocznej, która jest prostopadła do krawędzi podstawy
24 lut 21:30
salamandra: Chodzi mi o ten kat prosty który zaznaczyłeś na rysunku 20:56
24 lut 21:32
salamandra:
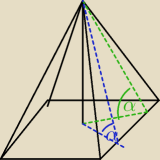
Przykładowo− ja nie widzę różnicy w takim czymś, bo przecież ściana w każdym miejscu jest
nachylona w moim mniemaniu pod takim samym kątem do podstawy− przechylę nie wiem− książkę
względem biurka, to nieważne skąd będę mierzył− kąt będzie identyczny
24 lut 21:45
wredulus_pospolitus:
oojjjjj nieeee

24 lut 21:46
salamandra: Definicję kąta dwuściennego znam, ale jakoś w tym przypadku nie potrafię sobie tego
przetłumaczyć, dlaczego te kąty się różnią, i ten kąt nachylenia ściany będzie akurat
"sterowany" w przypadku ostrosłupa dajmy na to prawidłowego czworokątnego, odcinkiem łączycym
spodek wysokości ze środkiem podstawy (połową wysokości podstawy)
24 lut 21:48
24 lut 21:50
wredulus_pospolitus:
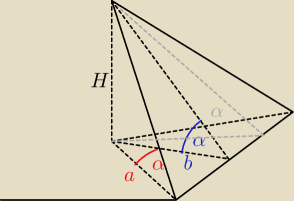
Czyli w Twoim mniemaniu
α =
α 
zauważ, że:
czyli
a =
b <−−− narysuj mi taki trójkąt (pamiętaj, że to dla dowolnego 'b' tutaj)
włącznie dla szarego miejsca
24 lut 21:51
salamandra: Milu− mówię, kąt dwuścienny rozumiem, ale głupio, powiedzmy sobie− głupio analizując jakieś
nachylenie książki do biurka nie potrafię sobię wyobrazić, że w różnych miejsach będzie różny
kąt nachylenia.
24 lut 21:51
salamandra: Tak wredulus, dokładnie− wczoraj nawet zacząłem sobie w głowie analizować, dlaczego kąt
nachylenia ściany do plaszczyzny podstawy się różni od kąta nachylenia KRAWĘDZI bocznej do
podstawy, wiem, że to są głupie pytanie i mógłbym po prostu zapamiętać jak jest i tyle, ale
nie tędy droga.
24 lut 21:52
Mila:
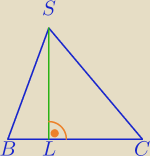
24 lut 21:53
wredulus_pospolitus:
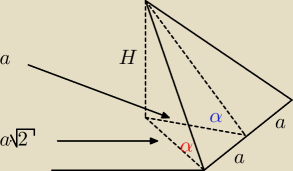
albo jak wolisz
mamy ostrosłup PRAWIDŁOWY czworokątny (kwadrat w podstawie) ... czy prawdą jest że:
α =
α 
24 lut 21:54
salamandra: według mojego idiotycznego filozofowania− tak.
24 lut 21:56
salamandra: jednak ten kwadrat mnie przekonał

24 lut 21:56
wredulus_pospolitus:
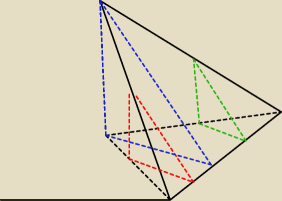
jednakowe kąty będą dla takich trójkątów (powtarzam rysunek z 21:24
gdzie czarne przerywane linie to połowy przekątnych tego rombu (czyli także kwadratu)
zauważ, że boki tych kolorowych trójkątów są wzajemnie (na danej płaszczyźnie) równoległe do
siebie i tylko jeden z nich (niebieski) będzie zawierał wysokość ostrosłupa jako jeden z
boków.
24 lut 22:03
wredulus_pospolitus:
i oczywiście ... każdy z tych kolorowych trójkątów pokazuje kąt nachylenia ściany bocznej do
podstawy
24 lut 22:07
salamandra: dzięki ci bardzo.... ...
24 lut 22:16
salamandra: W ostrosłupie trójkątnym ABCS ściany ABC i BCS są trójkątami równobocznymi, których bok ma
długość a. Oblicz jaka powinna być miara kąta dwuściennego miedzy tymi scianami, aby objętość
była najwieksza.
1. Między którymi ścianami?
24 lut 22:19
salamandra: czy "a" nie będzie również wysokością tego ostrosłupa, bo zauważam, że jak go przekręcę w bok,
to AB będzie wysokością, a BCS podstawą
24 lut 22:21
salamandra:
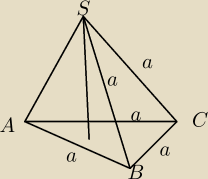
24 lut 22:22
wredulus_pospolitus:
pomiędzy tymi ścianami które są trójkątami równobocznymi ... w życiu ... 'a' nie będzie
wysokością tego ostrosłupa
wszystkie krawędzie boczne mają długość a (oraz dwa (na trzy) krawędzie postawy maja długość
'a' ) ... wysokość ostrosłupa nie może być równa długości krawędzi ściany każdej ze ścian
bocznych

24 lut 22:24
wredulus_pospolitus:
ten ostrosłup jest baaardzo podobny do tego z pierwszego postu ... zamień tylko '12' na '18' i
masz ten ostrosłup (dla a=18)
24 lut 22:25
salamandra: to ABC nie będzie podstawą?
24 lut 22:26
salamandra: Wybacz, ja już nie myślę dziś... przecież poza tymi zostaje mi tylko jedna krawędź..
24 lut 22:28
wredulus_pospolitus:
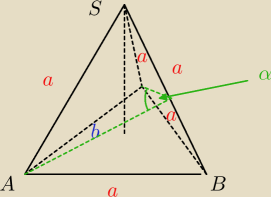
wyznaczamy α
uzależniamy 'b' od α i a
wyznaczamy objętość tego ostrosłupa
24 lut 22:30
salamandra: No dobra, ale jak dalej zrobić, bo przecież nie wiem de facto gdzie będzie wysokość tego
ostrosłupa, (nie mam wszystkich identycznych krawędzi bocznych, więc nie mogę z okręgu
opisanego), to jak wyznaczyć objętość?
24 lut 22:31
salamandra: (napisałem przed zobaczeniem odpowiedzi, już analizuję)
24 lut 22:31
wredulus_pospolitus:
Chwila ... AB
C i BCS

Na pewno

24 lut 22:31
salamandra: Tak, ABC i BCS
24 lut 22:32
salamandra: | | a3 | |
odpowiedź to: V(a)= |
| *sinα |
| | 8 | |
24 lut 22:39
wredulus_pospolitus:
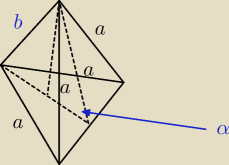 α
α jest to kąt pomiędzy dwoma wysokościami identycznych trójkątów równobocznych o boku 'a'
więc:
H
ostrosłupa = h
trójkąta równobocznego*sinα
Chociaż to trochę dziwne zadanie, bo wystarczy chwilę pomyśleć −−− P
p jest stałe (trójkąt
równoboczny), więc trzeba maksymalizować wysokość ostrosłupa, a wysokość będzie największa dla
kąta prostego (sinα = 1) i będzie równa wysokości podstawy
Jest to wniosek z powyższego wzoru.
24 lut 22:41
salamandra: wow, nawet dobrze wyznaczyłem H ostrosłupa.
Tylko ja założyłem (pewnie błędnie, ale wyszło dobrze), że operując moim rysunkiem− to kąt
między ścianą boczną BCS a płaszczyzną podstawy ABC
24 lut 22:43
wredulus_pospolitus:
to tak jakbyś miał ekierkę na krawędzi stołu ... kiedy ostrosłup będzie miał największą
objętość (gdzie ściana którą możesz poruszać to właśnie ekierka) ... wtedy gdy ekierka jest
prostopadła do stołu ... bo wtedy wysokość będzie największa

24 lut 22:44
wredulus_pospolitus:
No ale ja też zaznaczyłem dokładnie ten sam kąt ... pomiędzy podstawą (podstawa to też ściana

) a ścianą boczną
24 lut 22:45
salamandra: czyli innymi słowy− aż wysokość ściany bocznej będzie również wysokością ostrosłupa odpowiednio
wydłużając tę wysokość?
24 lut 22:46
wredulus_pospolitus:
A nawet gdyby chodziło o sytuację taką jak na rysunku z 22:30 to i tak możesz wtedy 'położyć'
ostrosłup na innej ścianie, tak że dostaniesz rysunek z 22:41
24 lut 22:46
salamandra: Tylko ciezko to sobie wyobrazic ze wydluzajac tę wysokosc nagle ten ostrosłup (ściana boczna)
zacznie się "prostować"
24 lut 22:47
wredulus_pospolitus:
Dokładnie.
24 lut 22:47
wredulus_pospolitus: weź do łapki ekierkę i sobie nią 'poruszaj' trzymając jeden bok ekierki na stole
24 lut 22:47
salamandra:
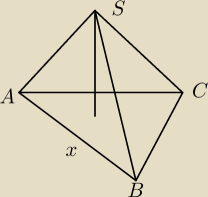
ostatnie zadanie......
W czworościanie ABCS krawedzie AC,AS,BC,BS,CS mają te sama dlugosc równą 1.
Jaka powinna byc dlugosc krawedzi AB aby objetosc czworościanu była największa.
wszystkie oprócz AB mają 1. Znów problemem dla mnie jest nieszczęsna wysokość....
24 lut 22:54
salamandra: Niby wszystkie krawędzie boczne równe, więc środkiem będzie środek okręgu opisanego? ale co
dalej
24 lut 22:55
wredulus_pospolitus:
A przewróć ten ostrosłup tak, żeby podstawą było np. BCS
Narysuj ... podpisz długości krawędzi a później spójrz na rysunek z 22:41
24 lut 22:56
salamandra: | | 13 | | 1√3 | | √3 | |
wtedy R= |
| = |
| = |
| |
| | 12√3 | | 3 | | 3 | |
R
2+H
2=1
2
Jak nie tak, to się poddaję na dziś.
24 lut 23:01
wredulus_pospolitus:
Co

1) Masz wyznaczyć ile ma się równać 'x' (bok) aby objętość była największa.
2) Więc objętość ostrosłupa jest ZMIENNA (więc i wysokość ostrosłupa będzie zmienna)
Narysuj tak jak napisałem o 22:56 (pokaż rysunek)
24 lut 23:02
wredulus_pospolitus:
i jeszcze na kolor niebieski zaznacz te krawędzie które mają STAŁĄ długość (równą 1)
24 lut 23:03
salamandra:
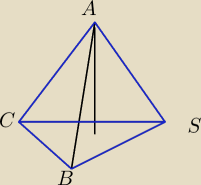
24 lut 23:06
wredulus_pospolitus:
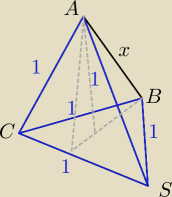
jedyne co się może zmieniać to DŁUGOŚĆ krawędzi |AB| = x
Kiedy objętość tego ostrosłupa będzie największa

Kiedy wysokość tego ostrosłupa będzie równa
ile

To w takim razie |AB| = x = ...

w takim przypadku

24 lut 23:09
salamandra: kiedy H=√3?
24 lut 23:13
wredulus_pospolitus:
| | a√3 | | √3 | |
kiedy H = htrójkąta równobocznego = |
| = |
| |
| | 2 | | 2 | |
24 lut 23:15
wredulus_pospolitus:
| | 3 | | √6 | |
wtedy x2 = 2(htrójkąta równobocznego)2 = |
| −> x = |
| |
| | 2 | | 2 | |
24 lut 23:16
salamandra: tak, chochlik,
bo będzie wtedy jak w poprzednim kąt prosty, więc wysokość ostrosłupa to wysokość ściany
bocznej (trójkąta równobocznego o boku 1, więc h=
√3)
| | √3 | | √3 | |
Wtedy z tw. Pitagorasa ( |
| )2+( |
| )2 = x2 |
| | 2 | | 2 | |
24 lut 23:17
salamandra: | | √3 | |
h= |
|  * |
| | 2 | |
24 lut 23:17
wredulus_pospolitus:
salamandra ... jak może wysokość ostrosłupa H =
√3 >1 = krawędź boczna ostrosłupa

Wysokość ostrosłupa = 'najkrótsza odległość' z wierzchołka do podstawy ostrosłupa
Krawędź ściany boczne = 'jakaś tam' odległość (przeważnie 'nie najkrótsza) z wierzchołka do
podstawy ostrosłupa
24 lut 23:18
salamandra: zapomniałem podzielić przez 2, i tyle
24 lut 23:19
salamandra: to z 23:17 to poirytowanie, że dwa razy ten sam chochlik przepisałem

24 lut 23:20
wredulus_pospolitus:
teraz ewentualnie spróbuj się zastanowić jak to zadanie rozwiązać bez 'przekładania' ostrosłupa
i bez zauważenia tego na czym polegało poprzednie zadanie.
24 lut 23:22
wredulus_pospolitus:
(wtedy trzeba się trochę napracować)
24 lut 23:23
Mila:
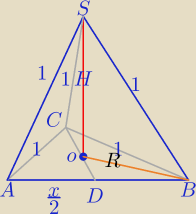
1) W ΔADC: CD=h
4−x
2>0 i x>0
| | 1 | | √4−x2 | | 1*1*x | |
2) PABC= |
| x* |
| = |
| |
| | 2 | | 2 | | 4R | |
R=...
3) H
2=1
2−R
2
i jesteś w domu, licz i napisz wynik
24 lut 23:23
salamandra: Muszę jeszcze jedno jednak zrobić...
Pole powierzchni ostrosłupa prawidłowego trójkątnego jest równe 12+
√3 a stosunek krawędzi
podstawy a do wysokości ściany bocznej h jest równy 1:2.
Oblicz pole P
b powierzchni bocznej tego ostrosłupa.
| | 1 | | 1 | | 3 | |
Pb=3*a* |
| a* |
| = |
| a2 |
| | 2 | | 2 | | 4 | |
Pc=Pp+Pb
I z tego znow nie chce wyjść....
24 lut 23:28
salamandra: Ok, złą proporcję wziąłem.
24 lut 23:29
Mila:
Dokończ to poprzednie zadanie wg 23:23 ( nomen omen)
24 lut 23:40
salamandra: Jutro, dziś już nie mam siły, 8h robić pracę domową to przesada....
dziękuję Wam za dzisiejszą pomoc..naprawdę...
24 lut 23:54
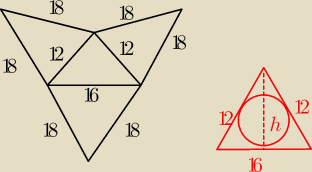 Na rysunku przedstawiono siatkę bryły. Nazwij tę bryłę. Oblicz pole powierzchni całkowitej oraz
objętość V
82+h2=122
h=4√5
Na rysunku przedstawiono siatkę bryły. Nazwij tę bryłę. Oblicz pole powierzchni całkowitej oraz
objętość V
82+h2=122
h=4√5




 teraz mam zadanie:
podstawą ostrosłupa jest romb, którego bok ma długość a, a krótsza przekątna ma długość d.
Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt α. Wyraź objętość tego ostrosłupa w
zależności od a,d i funkcji trygonometrycznej kąta α.
teraz mam zadanie:
podstawą ostrosłupa jest romb, którego bok ma długość a, a krótsza przekątna ma długość d.
Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt α. Wyraź objętość tego ostrosłupa w
zależności od a,d i funkcji trygonometrycznej kąta α.


 wiedziałem że jest wzór e*f*0,5*sinα, ale przecież α=90, a ja
sobie wpoiłem, że nie znam kąta więc z tego nie skorzystam...
wiedziałem że jest wzór e*f*0,5*sinα, ale przecież α=90, a ja
sobie wpoiłem, że nie znam kąta więc z tego nie skorzystam...


 salamndra , piszę rozwiązanie, tymczasem narysuj na kartce romb i wpisz w niego okrąg.
salamndra , piszę rozwiązanie, tymczasem narysuj na kartce romb i wpisz w niego okrąg.
 to co zaznaczyłeś to NIE JEST kąt α
to co zaznaczyłeś to NIE JEST kąt α

 czerwona linia to bok (na podstawie) szukanego trójkąta (czyli h/2), a nie niebieska
(czyli a/2)
czerwona linia to bok (na podstawie) szukanego trójkąta (czyli h/2), a nie niebieska
(czyli a/2)
 po
pierwszym rysunku już wiedziałem
po
pierwszym rysunku już wiedziałem
 |DB|=d
1) w ΔAOD:
|DB|=d
1) w ΔAOD:
 to jest kąt nachylenia ściany bocznej do podstawy
zauważ, że te wszystkie odcinki na ścianie bocznej są PROSTOPADŁE do krawędzi podstawy.
Wyobraź sobie że mamy tą ścianę boczną i ją 'obniżamy (zmniejszamy wysokość ostrosłupa) ...
cały czas te odcinki na ścianie bocznej są prostopadłe do krawędzi podstawy podstawy.
W końcu h{
to jest kąt nachylenia ściany bocznej do podstawy
zauważ, że te wszystkie odcinki na ścianie bocznej są PROSTOPADŁE do krawędzi podstawy.
Wyobraź sobie że mamy tą ścianę boczną i ją 'obniżamy (zmniejszamy wysokość ostrosłupa) ...
cały czas te odcinki na ścianie bocznej są prostopadłe do krawędzi podstawy podstawy.
W końcu h{ strosłupa] = 0 ... cały czas te odcinki są prostopadłe do podstawy ... czyli ten
środkowy odcinek to nic innego jak wysokość trójkąta wyznaczonego przez podstawę i połowy
przekątnych −−− czyli połowa wysokość rombu
strosłupa] = 0 ... cały czas te odcinki są prostopadłe do podstawy ... czyli ten
środkowy odcinek to nic innego jak wysokość trójkąta wyznaczonego przez podstawę i połowy
przekątnych −−− czyli połowa wysokość rombu

 Przykładowo− ja nie widzę różnicy w takim czymś, bo przecież ściana w każdym miejscu jest
nachylona w moim mniemaniu pod takim samym kątem do podstawy− przechylę nie wiem− książkę
względem biurka, to nieważne skąd będę mierzył− kąt będzie identyczny
Przykładowo− ja nie widzę różnicy w takim czymś, bo przecież ściana w każdym miejscu jest
nachylona w moim mniemaniu pod takim samym kątem do podstawy− przechylę nie wiem− książkę
względem biurka, to nieważne skąd będę mierzył− kąt będzie identyczny

 Czyli w Twoim mniemaniu
α = α
Czyli w Twoim mniemaniu
α = α  zauważ, że:
zauważ, że:
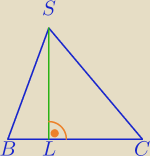
 albo jak wolisz
mamy ostrosłup PRAWIDŁOWY czworokątny (kwadrat w podstawie) ... czy prawdą jest że: α =
α
albo jak wolisz
mamy ostrosłup PRAWIDŁOWY czworokątny (kwadrat w podstawie) ... czy prawdą jest że: α =
α 

 jednakowe kąty będą dla takich trójkątów (powtarzam rysunek z 21:24
gdzie czarne przerywane linie to połowy przekątnych tego rombu (czyli także kwadratu)
zauważ, że boki tych kolorowych trójkątów są wzajemnie (na danej płaszczyźnie) równoległe do
siebie i tylko jeden z nich (niebieski) będzie zawierał wysokość ostrosłupa jako jeden z
boków.
jednakowe kąty będą dla takich trójkątów (powtarzam rysunek z 21:24
gdzie czarne przerywane linie to połowy przekątnych tego rombu (czyli także kwadratu)
zauważ, że boki tych kolorowych trójkątów są wzajemnie (na danej płaszczyźnie) równoległe do
siebie i tylko jeden z nich (niebieski) będzie zawierał wysokość ostrosłupa jako jeden z
boków.


 wyznaczamy α
uzależniamy 'b' od α i a
wyznaczamy objętość tego ostrosłupa
wyznaczamy α
uzależniamy 'b' od α i a
wyznaczamy objętość tego ostrosłupa
 Na pewno
Na pewno 
 α jest to kąt pomiędzy dwoma wysokościami identycznych trójkątów równobocznych o boku 'a'
więc:
Hostrosłupa = htrójkąta równobocznego*sinα
Chociaż to trochę dziwne zadanie, bo wystarczy chwilę pomyśleć −−− Pp jest stałe (trójkąt
równoboczny), więc trzeba maksymalizować wysokość ostrosłupa, a wysokość będzie największa dla
kąta prostego (sinα = 1) i będzie równa wysokości podstawy
Jest to wniosek z powyższego wzoru.
α jest to kąt pomiędzy dwoma wysokościami identycznych trójkątów równobocznych o boku 'a'
więc:
Hostrosłupa = htrójkąta równobocznego*sinα
Chociaż to trochę dziwne zadanie, bo wystarczy chwilę pomyśleć −−− Pp jest stałe (trójkąt
równoboczny), więc trzeba maksymalizować wysokość ostrosłupa, a wysokość będzie największa dla
kąta prostego (sinα = 1) i będzie równa wysokości podstawy
Jest to wniosek z powyższego wzoru.

 ) a ścianą boczną
) a ścianą boczną
 ostatnie zadanie......
W czworościanie ABCS krawedzie AC,AS,BC,BS,CS mają te sama dlugosc równą 1.
Jaka powinna byc dlugosc krawedzi AB aby objetosc czworościanu była największa.
wszystkie oprócz AB mają 1. Znów problemem dla mnie jest nieszczęsna wysokość....
ostatnie zadanie......
W czworościanie ABCS krawedzie AC,AS,BC,BS,CS mają te sama dlugosc równą 1.
Jaka powinna byc dlugosc krawedzi AB aby objetosc czworościanu była największa.
wszystkie oprócz AB mają 1. Znów problemem dla mnie jest nieszczęsna wysokość....
 1) Masz wyznaczyć ile ma się równać 'x' (bok) aby objętość była największa.
2) Więc objętość ostrosłupa jest ZMIENNA (więc i wysokość ostrosłupa będzie zmienna)
Narysuj tak jak napisałem o 22:56 (pokaż rysunek)
1) Masz wyznaczyć ile ma się równać 'x' (bok) aby objętość była największa.
2) Więc objętość ostrosłupa jest ZMIENNA (więc i wysokość ostrosłupa będzie zmienna)
Narysuj tak jak napisałem o 22:56 (pokaż rysunek)

 jedyne co się może zmieniać to DŁUGOŚĆ krawędzi |AB| = x
Kiedy objętość tego ostrosłupa będzie największa
jedyne co się może zmieniać to DŁUGOŚĆ krawędzi |AB| = x
Kiedy objętość tego ostrosłupa będzie największa Kiedy wysokość tego ostrosłupa będzie równa
ile
Kiedy wysokość tego ostrosłupa będzie równa
ile  To w takim razie |AB| = x = ...
To w takim razie |AB| = x = ...  w takim przypadku
w takim przypadku 
 *
* Wysokość ostrosłupa = 'najkrótsza odległość' z wierzchołka do podstawy ostrosłupa
Krawędź ściany boczne = 'jakaś tam' odległość (przeważnie 'nie najkrótsza) z wierzchołka do
podstawy ostrosłupa
Wysokość ostrosłupa = 'najkrótsza odległość' z wierzchołka do podstawy ostrosłupa
Krawędź ściany boczne = 'jakaś tam' odległość (przeważnie 'nie najkrótsza) z wierzchołka do
podstawy ostrosłupa

 1) W ΔADC: CD=h
1) W ΔADC: CD=h