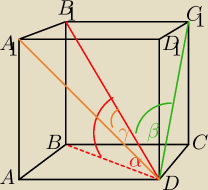
stereometria salamandra: Proszę o Wasz punkt widzenia na temat tych kątów. Od lekcji zastanawiam się i próbuję sobie wyobrazić te kąty i nie mogę tego pojąć. Jest zadanie: Przekątna BD₁β prostopadłościanu ABCDA₁B₁C₁D₁ tworzy ze ścianami o wspólnym wierzchołku D kąty α, β, γ. Wykaż, że cos²α+cos²β+cos²γ = 2 Nie potrafię zrozumieć, że ta zielona przekątna idzie po ścianie bocznej, nadal mam wyobrażenie jakby ona rzekomo szła "w środku" od punktu D do C₁, analogicznie z pomarańczową. Samo zadanie już rozwiązać umiem, ale nie potrafię zrozumieć, że te odcinki pomarańczowy i zielony przechodzą akurat przez ścianę boczną (są przekątnymi ściany bocznej). Do czerwonego oczywiście nie mam wątpliwości.

a@b: Rysuj "kreski" w pokoju na ścianach , na suficie i na podłodze To zobaczysz kąty proste !

salamandra: Nie chodzi mi w tym wypadku stricte o kąty proste, ale dlaczego ta zielona idzie po ścianie bocznej, a nie "wewnątrz" graniastosłupa?

a@b: Chyba ,że masz kulisty pokój To idź do koleżanki

a@b: Jak ze ścianami , to ..... z przekątnymi ścian ( bo ściany są kwadratami)

a@b: Jakbyś nie obracał tego sześcianu to kąty między przekątnymi w podstawie i ścianach bocznych Pojęte ?

a@b: Za to należy winić nauczycieli, którzy nie pokazują wam na modelach takich zależności !

Mila: Zgadzam się. Należy pokazywać modele szkieletowe i kąty widać.

a@b: Proponuję skorzystać z "Geo−gebry"

a@b: dla Mili

salamandra: Pokazuje, nawet polecał przekręcać itp, ale ja po prostu nie mam wyobraźni przestrzennej dlatego tyle pytań na ten temat zadaję

salamandra: Akurat to zadanie to miałem wytłumaczone opcjonalnie na zasadzie, żeby przekręcać ten prostopadłościan i te kąty będa identycznie ułożone jak α, ale mówię, nie mam wyobraźni. Natomiast spojrzałem na ścianę w pokoju i uświadomiłem sobie, że nie ma jak od wierzchołka tej samej ściany, poprowadzic przekątnej nie idąc po ścianie

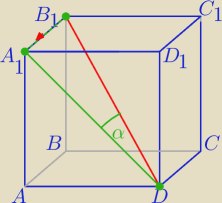
Mila: Kąt między przekątną DB₁ i ścianą ADD₁A₁ to kąt między DB₁ i rzutem prostokątnym tej przekątnej na ścianę ADD₁A₁ . Rzutem D jest ten sam punkt, rzutem drugiego końca (B₁) jest punkt A₁. Rzutem DB₁ jest odcinek DA₁. α −kąt między przekątną DB₁ i ścianą ADD₁A₁

salamandra: W związku z tym B₁A₁D będzie prosty?

a@b: no taaaaaaaaaaaaaaaaaaaaaaaaaaaak

salamandra: Wybaczcie Panie, żem tak oporny jest z tymi bryłkami. I tak już powinienem na rękach nosić, ale do tego maja jeszcze pomęczę Teraz rozważam pomarańczową przekątną: B₁A₁D prosty W czerwonej B₁BD

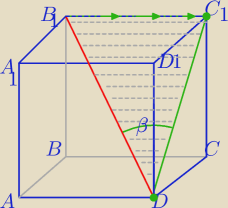
Mila: Kąt między przekątną DB1 i ścianą DCC₁D1 to kąt między DB1 i rzutem prostokątnym tej przekątnej na ścianę DCC₁D1. β − kąt między przekątną DB1 i ścianą DCC₁D1

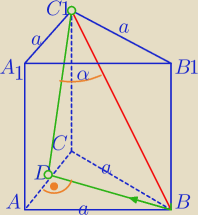
Mila: Graniastosłup prawidłowy trójkątny. Kąt między przekątną ściany bocznej i sąsiednią ścianą boczną np. ACC₁A₁− to kąt między tą przekątną i jej rzutem na ścianę ACC₁A₁. ♦ Rzutem punktu C₁ jest C1. ♦ Rzutem prostokątnym punktu B jest punkt D α − kąt między przekątną (BC₁) ściany bocznej i sąsiednią ścianą boczną ACC₁A₁ Eta ładnie to rysuje z przewróconym graniastosłupem. Wtedy lepiej widać.

xyz: A potrafil by ktos narysowac ostroslup o podstawie kwadratowej (nie prosty) gdzie spodek wysokosci znjduje sie w jednym z wierzcholkow i znalezc kat nachylenia scian bocznych. ktore nie zawieraja wysokosci ostroslupa do plaszczyzny podstawy? Kompletnie nie widze tego kata, jak to rzucic? @Mila dalabys rade to zrobic i opisac jak tu wyzej?

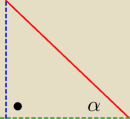
salamandra: Lubię tłumaczenie na zasadzie długopisa i rzucanego przez niego cienia, założmy hipotetycznie, że czerwone to długopis, zielone to cień, a niebieskie to odcinek rzutujący. Czy dobrze oznaczyłem?

Mila: xyz narysuję, ale wolałabym konkretne zadanie, bo nie wiem czy utrafię z treścią. Za godzinkę będę Napisz treść , albo ja wg własnego uznania napiszę uwzględniając to, co już napisałeś 18:52 ?

salamandra: Milu, a w Twoim rysunku z 18:38, kąt DBC₁ to co to byłby za kąt? między czym, a czym?

Mila: kąt DBC1 − kąt między przekątną ściany bocznej i wysokością podstawy.

salamandra: A wracając do tego mojego "doświadczenia" z długopisem?

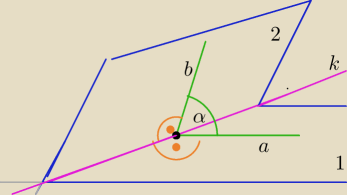
Mila: Dla xyz Aby zaznaczyć kąt pomiędzy ścianami (zwany kątem dwuściennym) znajdujemy najpierw wspólną krawędź tych dwóch ścian. (k) Następnie do wybranego punktu na tej krawędzi prowadzimy dwa odcinki, jeden zawarty w pierwszej ścianie, drugi – w drugiej, tak aby były one prostopadłe do tej krawędzi. a⊥k, b⊥k α − Kąt pomiędzy tymi odcinkami to kąt dwuścienny (czyli kąt pomiędzy tymi ścianami):

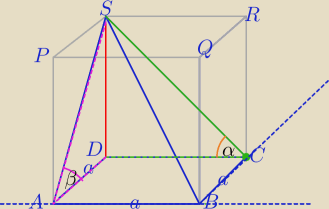
Mila: Dla xyz. ABCD − kwadrat. Odcinek SD prostopadły do płaszczyzny podstawy (ABCD) 1) ΔADS prostopadły do ABCD ΔCDS prostopadły do ABCD Odcinek BC jest prostopadły do płaszczyzny DCRS to jest prostopadły do CS. BC⊥CS BA⊥AS 2) BC− wspólna krawędź płaszczyzn ABCD i BCS Odcinek SC jest prostopadły do krawędzi (BC) dwóch płaszczyzn ABCD i SBC. odcinek DC jest prostopadły do krawędzi (BC) dwóch płaszczyzn ABCD i SBC. α− kąt między ścianą boczną SBC a płaszczyzną podstawy ABCD 3) AB − wspólna krawędź płaszczyzn ABCD i ABS Odcinek AS jest prostopadły do wspólnej krawędzi (AB) dwóch płaszczyzn ABCD i ABS. odcinek DA jest prostopadły do krawędzi (AB) dwóch płaszczyzn ABCD i ABS β− kąt między ścianą boczną ABS a płaszczyzną podstawy ABCD

Mila: salamandra zaznaczyłeś kąt między odcinkiem ( czerwonym) a rzutem prost. ( zielonym) 18.56

salamandra: Czyli rzut prostokątny = cień rzucany na biurko, a ten odcinek, to mój długopis, a niebieskie to odcinek rzutujący?

Mila: Tak, przecież to Ci już tłumaczyłam. Po co ja robię rysunki , nie oglądasz i nie czytasz?

xyz: Milu dziękuję Ci bardzo serdecznie i w sumie miałbym pytanie czy np. kąt alfa to też byłby kąt pomiędzy środkiem odcinka BC, a środkiem podstawy (w sensie odcinka łączącego środki odcinków tych wzdłuż)

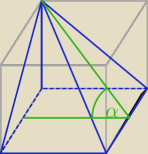
xyz: ten kąt

salamandra: Co rysunek to inny, a muszę mieć też pewność, że swoim tokiem rozumowania też rozumiem. Bo np. w przypadku 17:58 i 18:08, już nie jestem sobie w stanie na zasadzie tego długopisu wytłumaczyć, bo jak nachylę długopis od kątem rozwartym, to cień powstaje z drugiej strony (zakładając, że w 18:08 i 17:58 przekątna prostopadłościanu jest tym długopisem,

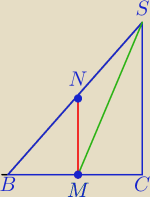
Mila: Nie. ΔBCS tak wygląda. Zielony odcinek nie jest prostopadły do BC. Rozpisałam dokładnie jak są położone odcinki względem siebie. Przeczytaj uważnie. M− środek BC MN⊥BC − Odcinek prostopadły do BC . Wtedy N jest w połowie BS i wtedy komplikują się dalsze obliczenia w zadaniu.

salamandra: Są już przypadki w których nie mam wątpliwości, nauczyciel sam mi powiedział, że jeszcze trochę i nawet nie będę się zastanawiał, tylko odruchowo to będę robił, chcę natomiast od samego początku stereometrii ją ogarnąć, bo to moja słabość i przed samą maturą nie chce juz sie tym martwic, że nie umiem elementarnych rzeczy z tego materiału