trójkat
mat-fiz:
Trójkąt równoboczny ABC zgięto wzdłuż prostej EF, E∊AC i F∊BC
tak,że wierzchołek C znalazł się w punkcie P na boku AB
dzieląc ten bok w stosunku 1:3 licząc od wierzchołka A
Wyznacz długość odcinka EF
21 lut 21:19
Blee:
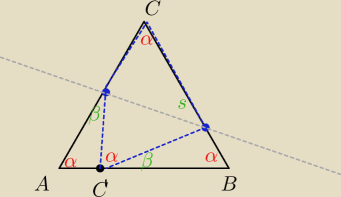
skorzystaj z podobieństwa trójkątów AEC' i BC'F w celu uzyskania informacji gdzie leżą E i F na
bokach tego trójkąta
później możesz użyć chociażby tw. cosinusów (α = 60
o)
21 lut 21:51
21 lut 22:11
Blee:
a mi się nie chciało tego liczyć
21 lut 22:11
a@b:
I to nie jest takie sobie "chop−siup" ... kochaniutki
Blee 
21 lut 22:11
a@b:
To,że jesteś
leniwy, to wie prawie ......
21 lut 22:13
salamandra: Mój emerytowany już nauczyciel fizyki i informatyki powiedział kiedyś, że najbardziej leniwi
są: matematycy, informatycy, a najbardziej fizycy
21 lut 22:17
a@b:
Ciekawe czy taką też odp: ma
Mila (
pracowita jak pszczółka 
21 lut 22:17
a@b:
Hehe ... to co powiesz o naszej
Mili
21 lut 22:19
salamandra: Wyjątki nie stanowią reguły
(ja również jestem leniwy)
może nie miał na myśli płci żeńskiej
21 lut 22:20
a@b:
Wniosek:
wszystkie chłopy .... to leniwce!
21 lut 22:22
Saizou :
| | 13√39 | |
Nie zgadzam się, przeliczyłem to zadanie, ale wyszedł mi inny wynik ( |
| ). |
| | 35 | |
Raz jeszcze policzę
21 lut 22:23
a@b:
Ja oczywiście liczyłam z trójkątów "ekierkowych "
Może się gdziesik rąbnęłam
Licz
Saizou jeszcze raz .... i zobaczymy
21 lut 22:26
Blee:
nie jest ... no dobra ... przyjmuję wyzwanie
oznaczenia:
x = |AC'|
z = |AE|
y = |BF|
z ΔAEC' (tw. cosinusów)
| | 15 | |
(4x−z)2 = x2 + z2 − xz −> 15x2 − 7xz = 0 −> x(15x − 7z) = 0 −> z = |
| x |
| | 7 | |
| | 13 | |
więc |CE| = 4x − z = |
| x |
| | 7 | |
z ΔBFC' (tw. cosinusów)
| | 7 | |
(4x−y)2 = (3x)2 + y2 − 3xz −> 7x2 − 5xy = 0 −> x(7x − 5y) = 0 −> y = |
| x |
| | 5 | |
| | 13 | |
więc |CF| = 4x − y = |
| x |
| | 5 | |
i ostatnie tw. cosinusów:
| | 169 | | 169 | | 169 | |
(|EF|)2 = ( |
| + |
| − |
| )x2 = |
| | 49 | | 25 | | 35 | |
| | 52 + 72 − 5*7 | | 13x | |
= 132x2* |
| = ( |
| )2*39 |
| | 7252 | | 35 | |
| | 13√39 | | 13√39 | |
|EF| = |
| x = |
| |AB| |
| | 35 | | 140 | |
21 lut 22:27
Blee:
Saizou −−− nie podzieliłeś przez 4 na końcu
... zauważ, ze Twój wynik: 13
√39 > 13*4 > 35
więc z tego wynikałoby, jakoby |EF| > boku trójkąta
Poza tym −−− wyszło mi tyle samo
21 lut 22:29
Blee:
niech ewentualnie ktoś usunie moje obliczenia (co by nie psuć maturzyście 'zabawy' )
21 lut 22:29
a@b:
Trzy wyniki i..... każdy inny
Czekam na
Milę 
Fajnie, że
chłopom zawsze można wejść na ambicję
21 lut 22:30
Saizou :
Źle wklepałem do komputera (zapomniałem przepisać |AB|)
21 lut 22:31
ite: a@b nie ma chłopów leniwców, są tylko niezagonieni do roboty (obecnie nazywa się to
zewnętrzną mobilizacją)
21 lut 22:31
Blee:
a@b jak inny ... Saizou ma (prawie) to samo co ja ... po prostu nie podzielił przez 4 ...
niestety −−− szukaj błędu u siebie
21 lut 22:33
Saizou :
| | 13√39 | | 13√39 | |
miałem taki zapis |
| a (a=|AC'|) → |
| |AB| |
| | 35 | | 140 | |
21 lut 22:34
a@b:
Nie mam błędu!
i nie chce być inaczej
21 lut 22:35
Blee:
to pokazuj obliczenia
21 lut 22:38
a@b:
Już się maluje
( chwila, moment)
21 lut 22:40
Blee:
to ja idę zapalić
21 lut 22:40
Blee:
Saizou −−− z ciekawości −−− korzystałeś z podobieństwa czy też po prostu leciałeś z tw.
cosinusów
21 lut 22:40
Blee:
chwila a@b ... liczyłaś z trójkątów ekierkowych? dlaczego przyjęłaś, że ∡AC'E = 90
o na
jakiej podstawie
21 lut 22:47
a@b:
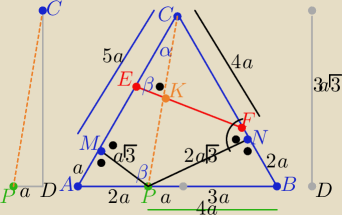
1/ korzystam z trójkątów ekierek :30
o,60
o, 90
o ( oznaczenia jak na rys.
|PC|= 2a
√7 to |PK|=|KC|=
√7
2/ z podobieństwa trójkątów
PMC i EKC oraz PNC i FKC
| a√3 | | EK | | 2a√3 | | KF | |
| = |
| oraz |
| = |
| |
| 5a | | √7 | | 4a | | 4a | |
EK=
√21a/5 KF=
√21a/2
| | 7√21 | |
|EF|= |
| a , gdzie |AB|=6a |
| | 10 | |
to
21 lut 22:57
a@b:
Na takiej podstawie,że
CE=EP Δ CEP równoramienny ( to chyba oczywista −oczywistość !
21 lut 22:59
Blee:
punkt P błędnie wyznaczony ... stosunek długości to NIE JEST 2a : 4a czyli 1:2 tylko 1:3
21 lut 23:01
a@b:
2a:6a =1:3
21 lut 23:05
Blee: a@b −−− szkolny błąd:
treść zadania: "dzieląc ten bok w stosunku 1:3 "
czyli mamy bok podzielony na części x : 3x ... więc bok jest długości x+3x = 4x
21 lut 23:07
a@b:
Przeczytałam AP:AB 1:3
sorry
21 lut 23:09
Saizou :
Raz tak, raz tak. Liczyłem dwa razy
21 lut 23:12
a@b:
Saizou już wszystko jasne
źle przeczytałam treść
21 lut 23:13
21 lut 23:13
Saizou :
Eta to
na zdrowie
21 lut 23:14
Mila:
Mój wynik jak we wpisie 22: 34
22 lut 16:28
Mila:
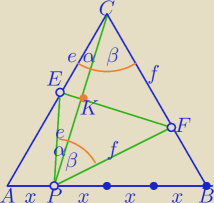
Podpowiedź dla maturzysty, inny sposób niż podane wyżej.
1) |CP|=x
√13
2) W ΔPBC: z tw. sinusów
3) W ΔAPC: z tw.sinusów
22 lut 18:30