pytanie
pytająca: W zadaniach tego typu :
397016. Skąd mam wiedzieć która funkcja jest ograniczeniem
gornym, a która dolnym?
Jest jakaś zasada na to(oprócz domyślania się z wykresu)?
12 lut 12:45
Jerzy:
Z wykresu.
12 lut 13:02
Blee:
Ta co jest 'wyżej' jest ograniczeniem górnym, ta co jest 'niżej' jest ograniczeniem dolnym
12 lut 13:10
Blee:
dlatego też zadania z całki oznaczonej zaczyna się od ... wykonania wykresu
12 lut 13:11
pytająca: A nie ma innych sposobów bo ja tego nie widzę?
I kiedy się dodaje do całkowitego pola obszaru, pole obszaru ujemnego?
12 lut 13:11
Jerzy:
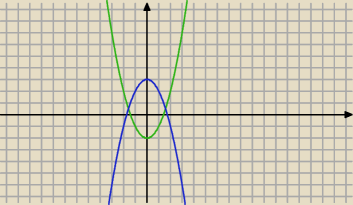
Nic nie dodajesz. To się "dodaje samo".
Niebieska górna, zielona dolna.
12 lut 13:13
pytająca: Dla 3 i więcej funkcji też się nie uwzględnia ujemnego obszaru?
12 lut 13:18
Blee:
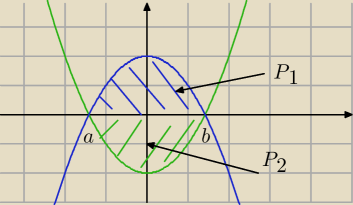
Jak Jerzy napisał −−− nic nie dodajesz/odejmujesz
Przykładowo ... masz obliczyć to pole (niebieskie + zielone)
∫
ab (−x
2 + 2) − (x
2 − 2) dx = (*)
rozwiązując tą całkę otrzymasz wynik:
(*) = P
1 − (−P
2) = P
1 + P
2 (jako ,że pole P
2 jest poniżej osi OX to wynik całki
wyjdzie ujemny ... dwa minusy dają plus)
12 lut 13:19
Jerzy:
Nie ma pojęcia "obszar ujemny". Obszar może leżeć pod osia OX, ale nie może być ujemny.
12 lut 13:19
pytająca: Tylko traktuje się go jakby był dodatni. Dlatego całka z niego jest dodatnia? Dobrze myślę?
12 lut 13:19
pytająca: Już wiem dziękuję!
12 lut 13:21
Blee:
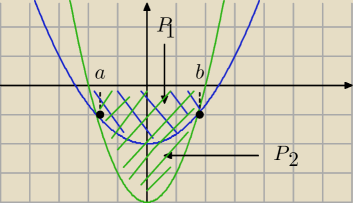
Inny przykład
∫
ab (x
2/3 − 2) − (x
2 − 4) dx = (−P
1) − (−P
1 − P
2) = P
2 <−−− czyli pole szukanego
obszaru pomiędzy tymi dwoma funkcjami
12 lut 13:23
Blee:
Po prostu gdy masz więcej niż dwie funkcje (jak w tamtym przykładzie) to musisz podzielić
granice całkowania (i dobrać odpowiednie funkcje) tak aby liczyć ten obszar który chcesz −−−
patrz to co napisałem w tamtym temacie
12 lut 13:25
Blee:
∫
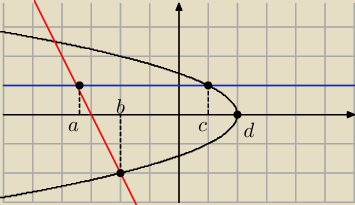
ab niebieska −
czerwona dx + ∫
bc niebieska −
'ujemna' czarna dx +
∫
cd 'dodatnia' czarna −
'ujemna' czarna dx = ...
12 lut 13:29
pytająca: Dziękuję jeszcze raz
12 lut 13:42
pytająca: Jeszcze jedno pytanie: może wyjść całkowite pole obszaru ujemne?
12 lut 15:36
Blee:
NIE
12 lut 15:37
pytająca: Np. w takim zadaniu wychodzi mi ujemne:
| | 1 | |
Dane są funkcje: f(x)=x2,g(x)= |
| x2,b(x)=3x oblicz pole ograniczone przez tę funkcję. |
| | 2 | |
Pole wychodzi mi −3.5
12 lut 15:47
pytająca: | | 4 | |
Przy takich też: h(x)=1,m(x)= |
| |
| | x2+1 | |
12 lut 15:48
pytająca: Przy tym drugim −2√3
12 lut 15:49
pytająca: Co mam źle?
12 lut 16:01
Blee:
nie wiem ... bo nie wiem CO liczysz
12 lut 16:02
Jerzy:
Pokaż co i jak liczysz ?
12 lut 16:05
Blee:
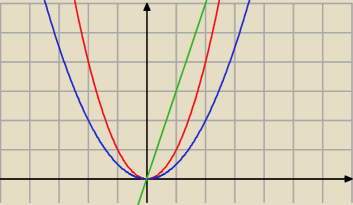
1)
∫
0a (x
2 − x
2/2) dx + ∫
ab (3x − x
2/2) dx
gdzie a=3 i b=6 to punkty przecięcia prostej y = 3x tychże parabol
12 lut 16:05
Blee:
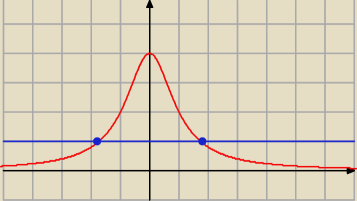
gdzie a = −
√3 ; b =
√3
12 lut 16:07
pytająca: Dzielę obszar D w pierwszym na obszar(P
1) ograniczony przez f(x)i g(x) oraz obszar (P
2)
ograniczony przez f(x) i g(x).
Granice całkowania są takie same a=0,b=3 gdzie a−dolna,b−gorna
| | 1 | |
Wychodzą mi pole : P=P1+P2=∫x2−3xdx+∫x2− |
| x2 |
| | 2 | |
12 lut 16:08
Blee:
nie ten obszar masz liczyć
po drugie −−− pierwsza całka −−− tutaj pojawia się ten minus ... źle ograniczenia zrobione
(która funkcja jest 'wyżej'
A która odejmujesz
12 lut 16:10
pytająca: Ok czyli cały obszar biorę ? Bo nie było określone czy y=1 to ograniczenie z góry czy z dołu
Tak samo w tym pierwszy zadaniu : nie wiadomo czy brać cały obszar czy tylko jego część.
12 lut 16:11
pytająca: Czyli tylko ten P1 −najbardziej wewnętrzny?
12 lut 16:12
Blee:
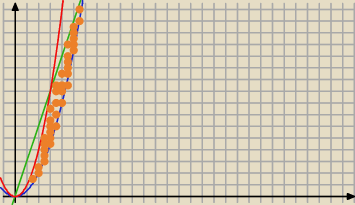
ten obszar masz policzyć
12 lut 16:12
Blee:
masz obliczyć obszar POMIĘDZY krzywymi
w drugim zadaniu jaki (skończony) obszar jest ograniczone przez te dwie funkcje
12 lut 16:14
pytająca: Ok dziękuję bardzo
12 lut 16:15
pytająca: W drugim już wiem
12 lut 16:15