wykres
licbaza: zaznacz na płaszczyźnie: x < |y|, x ≥ |y|, |x| < y
trochę nie rozumiem tego, próbowałem z definicji wartości bezwzględnej dla y, ale dalej nie
wychodzi
czemu np. jak mamy x < −y dla y < 0 − z definicji, to nie trzymamy się tego, by y < 0? wiem, że
wykresem czegoś takiego jest wszystko to, co pod prostą y = −x, ale nie rozumiem dlaczego
11 lut 19:08
Jerzy:
Jeżeli y = −x ,to np.punkt (−1,1) leży na tej prostej,a teraz popatrz, gdzie leży punkt
(−1,1/2).
11 lut 19:24
licbaza: hmm, no pod tą prostą. więc wtedy x < −y. tylko jakbym chciał wg definicji to rozpatrywać, to
biorę rozbijam na przedziały y < 0 i y ≥ 0. no i teraz biorę x < −y dla y < 0. więc powinienem
brać sprawdzać y < 0, a tu mamy y > 0
11 lut 19:34
Jerzy:
Tutaj błądzisz. Jeśli y < 0 , to |x| < y jest nierównością sprzeczną, bo |x| ≥ 0
11 lut 20:00
licbaza: no i właśnie tu jest błąd. jak to sobie inaczej wyobrazić, pomijając interpretację
geometryczną?
11 lut 20:13
Mila:
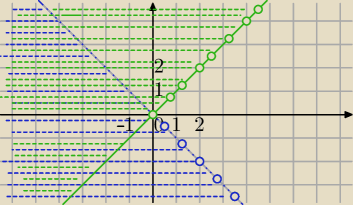
1)
x < |y|⇔
|y|>x⇔y<−x lub y>x
Zbiór punktów poniżej prostej y=−x lub powyżej prostej y=x
(suma obszarów)
11 lut 20:14
Mila:
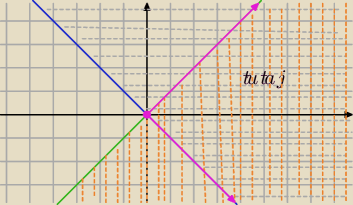
2) |y|≤x
−x≤y≤x
y≥−x − zbiór punktów leżących na prostej y=−x i powyżej tej prostej
i
y≤x − zbiór punktów leżących na prostej y=x i poniżej tej prostej
(część wspólna
11 lut 20:24
Mila:
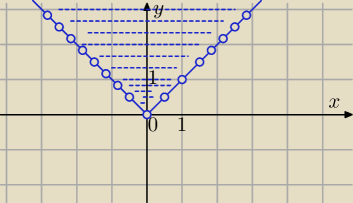
3)
|x| < y
y>|x|
11 lut 20:27
licbaza: dziękuję, spróbuję to przeanalizować i jakoś przetrawić

11 lut 20:52
Mila:

11 lut 22:17
11 lut 22:20
 1)
x < |y|⇔
|y|>x⇔y<−x lub y>x
Zbiór punktów poniżej prostej y=−x lub powyżej prostej y=x
(suma obszarów)
1)
x < |y|⇔
|y|>x⇔y<−x lub y>x
Zbiór punktów poniżej prostej y=−x lub powyżej prostej y=x
(suma obszarów)
 2) |y|≤x
−x≤y≤x
y≥−x − zbiór punktów leżących na prostej y=−x i powyżej tej prostej
i
y≤x − zbiór punktów leżących na prostej y=x i poniżej tej prostej
(część wspólna
2) |y|≤x
−x≤y≤x
y≥−x − zbiór punktów leżących na prostej y=−x i powyżej tej prostej
i
y≤x − zbiór punktów leżących na prostej y=x i poniżej tej prostej
(część wspólna
 3)
|x| < y
y>|x|
3)
|x| < y
y>|x|

