Test wyboru Statystyka
Konrad: Prosiłbym o pomoc w rozwiązaniu tego teściku
1.Zmienna losowa X podlega rozkładowi normalnemu z wartością średnią 55 i odchyleniem
standardowym 5 Zatem:
a) P(X>60)=0
b)P(X<60)<0,5
c)P(X<60)>0,5
d)P(X=60)<0,5
2.Zmienna losowa X podlega rozkładowi normalnemu z wartością średnią 0 i odchyleniem
standardowym 5. Zatem:
a)P(x<0)=0
b)P(x<0)<0,5
c)P(x<1)>0,5
d)P(x>1)<0,5
3.Wartość oczekiwana standaryzowanej zmiennej losowej w rozkładzie normalnym wynosi:
a)1
b)0
c)p
d)n
4.Rozkład Poissona jest:
a)jednoparametryczny z parametrem n
b)jednoparametryczny z parametrem p
c)dwuparametryczny z parametrem n
d)żadna z wymienionych odpowiedzi
5.Aby zweryfikować hipotezę statystyczną głoszącą że więcej niż połowa studentów pije należy
zastosować test:
a)dla średniej
b)dla wskaźnika struktury
c)nieparametryczny
d)dla wariancji
6.Zastosowanie testu istotności T przy weryfikacji hipotezy statystycznej o średniej wymaga:
a)minimalnej liczebności próby
b)znajomości odchylenia standardowego σ
c)znajomości wskaźnika struktury p
d)znajomośći rozkładu zmiennej losowej.
2 sie 17:34
Bleee:
1) Skoro średnia masz 55... DOKLADNIE jest x<55 i x>55 więc która odpowiedź będzie prawidłowa?
2) DOKLADNIE na to samo kopyto zadanie tylko inna wartość sredniej
3) jaki jest STANDARDOWY rozkład normalny? N(.... i co tutaj jest....) i która z tych wartości
oznacza wartość oczekiwana?
4) popatrz na wzór rozkładu Poissona
5 i 6 to że statystyki której szczerze w ogóle nie pamietam
2 sie 20:07
Adamm:
Zero inicjatywy.
Zero znaczy null. Nic. Nie pomogę, mam związane ręce.
2 sie 20:58
pol: up
11 lut 22:06
Blee:
pol ... no jak a będzie odpowiedź na pierwsze pytanie?
Średnia wartość wynosi 55
| | 1 | |
Więc P(X<55) = P(X>55) = |
| bo to jest ŚREDNIA wartość w rozkładnie normalnym ... |
| | 2 | |
dokładnie połowa jest mniejsza i dokładnie połowa jest większa od tejże średniej w rozkładzie
normalnym.
Więc która z tych odpowiedzi będzie poprawna ( ... żeby nie było wątpliwości: 60 > 55 ... )
11 lut 22:47
pol: P(X<60)>0.5 tak Panie blee?
11 lut 23:05
Blee:
Dokładnie.
Więc teraz (2) analogicznie która odpowiedź będzie poprawna
12 lut 00:01
Blee:
To jest zadanie na to czy rozumiemy jak wygląda wykres gęstości rozkładu normalnego
12 lut 00:01
Blee:
Uwaga −−− w (2) zadaniu czeka na nas pewien 'psikus' (chyba że autor źle przepisał odpowiedzi)
12 lut 00:02
pol: P(X<0)>0.5
12 lut 00:18
Blee:
a dlaczego skoro EX = 0 (wartość średnia =0)
12 lut 00:40
pol: dobra to P(x<1)>0.5 robie to na "czuja"
12 lut 00:46
Blee:
Tak ... ale także P(X>1) < 0.5
No bo w końcu P(X<1) + P(X>1) = 1 co nie
12 lut 01:03
pol: to jeszcze takie srednia 55 odchylenie 5
a) P(x>40)=0 to mi tylko pasuje
b) P(X<40)=0,5
C) P(X=40)>0
D) P(X<40)<0.5
jaka
12 lut 01:07
pol: po co w ogóle podawali odchylenie jak z niego nie korzystamy ?
12 lut 01:07
Blee:
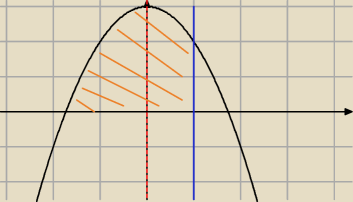
uwaga ... to oczywiście NIE JEST wykres gęstości rozkładu normalnego, ale ma posłużyć jako
pokazanie 'co i jak'
1) Jak widzimy ... dla EX = 0 dokładnie POŁOWA pola (prawdopodobieństwa) jest 'na lewo' od
średniej a połowa 'na prawo' od średniej
| | 1 | |
Stąd: P(X < EX) = P(X > EX) = |
| (zawsze to ma miejsce w rozkładzie normalnym) |
| | 2 | |
Więc jeżeli weźmiemy prawdopodobieństwo dla wartości większej niż EX to naturalne że
| | 1 | |
P(X < k) > P(X < EX) = |
| (gdzie k > EX) −−− patrz zaznaczony obszar |
| | 2 | |
| | 1 | |
a jednocześnie P(X > k) < P(X > EX) = |
| (co jest konsekwencją powyższego) |
| | 2 | |
12 lut 01:08
Blee:
Dla wprowadzenia dodatkowego zamętu
12 lut 01:09
Blee: jak tego 'nie czujesz'
to zrób szkic wykresu gęstości rozkładu normalnego (mam nadzieję, że wiesz jak on wygląda)
W 'piku' masz średnią (w tym przypadku x = 55) zaznacz sobie (tak pi razy oko) x = 40 .. rób
linię i patrzaj 'ile pola' jest 'na lewo' a ile 'na prawo' od tejże prostej x=40 (więcej czy
mnie niż połowa)
12 lut 01:11
Blee:
a) odpada ... P(X > 40)
> P(X > 55) (prawdopodobieństwo że wybrana liczba jest większa
od 40 jest na pewno większe od prawdopodobieństwa że będzie ona większa od 55, nieprawdaż ?!)
| | 1 | |
a P(X > 55) = |
| bo EX = 55 |
| | 2 | |
12 lut 01:12
Blee:
| | 1 | |
b) odpada ... bo |
| = P(X < 55) ... a przecież prawdopodobieństwo ze liczba jest mniejsza |
| | 2 | |
od 40 będzie MNIEJSZE od prawdopodobieństwa że liczba jest mniejsza od 55 (na logikę)
12 lut 01:13
Blee:
c) odpada ... to musisz sobie wbić do głowy, że w rozkładzie ciągłym P(X = k) = 0
(prawdopodobieństwo wylosowania tej KONKRETNEJ LICZBY jest równe zero)
nie powiem Ci które twierdzenie o tym mówi, nie pamiętam tego −−− musisz sprawdzić
12 lut 01:14
Blee:
więc zostaje jedynie (d)
no i faktycznie P(X<40) < P(X<55) (patrz opis z (b))
12 lut 01:15
pol: dzięki wielkie Dobry Człowieku, wszystkiego dobrego. pozdrawiam
12 lut 01:16
Blee:
Możesz też rozumowanie to przeprowadzać na wykresie dystrybuanty rozkładu normalnego, ale
wydaje mi się, że wykres gęstości jest bardziej rozpoznawalny (krzywa Gaussa) i szybciej sobie
skojarzysz jego kształt
12 lut 01:19
12 lut 01:20
pol: to dla pewności odpowiedzi do pozostałych zad 3 odp B 0 4 jednoparametryczny 5 b
12 lut 01:25
pol: 6a
12 lut 01:25
Blee:
4 −−− ale który jest parametrem? n czy p (co jest ciekawe .. bo ja nie wiem czym jest n i p
)
12 lut 01:30
Blee:
a 5 i 6 tak jak wcześniej pisałem −−− nie wiem −−− statystykę miałem dawno temu i nie używałem
(tej 'podstawowej' ) do niczego, więc nie mam bladego pojęcia
12 lut 01:31
pol: gówniane pytania pisane przez gimbusa
12 lut 01:31
pol: dzięki jeszcze raz Blee
12 lut 01:32
