| √3 | ||
Proszę o pomoc  . Jak zaznaczyć rozwiązania lub to rozwiązać. sin2x= | ||
| 2 |
| √3 | ||
sin2x=− | ||
| 2 |
| √3 | ||
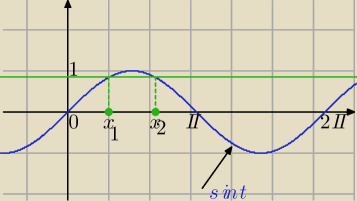
sint= | ||
| 2 |
| π | π | |||
odpowiedź na 14:26 | +2kπ ( π− | )+2kπ | ||
| 3 | 3 |
| √3 | √3 | √3 | ||||
2x= | /2 x= | lub x=− | ||||
| 2 | 4 | 4 |
| √3 | ||
sin(2x)= | ⇔ | |
| 2 |
| π | π | |||
2x= | +2kπ lub 2x=π− | +2kπ⇔ | ||
| 3 | 3 |
| π | 2π | |||
2x= | +2kπ lub 2x= | +2kπ /:2 | ||
| 3 | 3 |
| π | π | |||
x1= | +kπ lub x2= | +kπ | ||
| 6 | 3 |