Okręgi
salamandra: Napisz równanie okręgu przechodzącego przez punkty A i B gdzie A(3,0), B(−1, 2)
Którego środek leży na prostej o równaniu x−y+2=0.
Jedyne co wiem, to że AO = BO i że jest to promień gdzie O to środek okręgu, ale co dalej?
18 gru 13:22
Jerzy:
S = (y − 2,y)
(y − 2 − 3)2 + (y − 0)2 = (y − 2 + 1)2 + (y − 2)2 i obliczasz współrzędne środka i na
koncu promień.
18 gru 13:32
Tadeusz:
18 gru 13:36
Tadeusz:
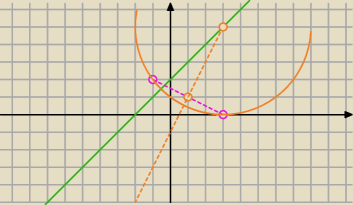
Znacznie upraszcza liczenie jeśli zauwazysz, że szukany okrąg jest styczny do Ox w punkcie A
wtedy współrzędne srodka masz niemal z automatu
18 gru 13:39
Blee:
@Tadeusz,
może i upraszcza, ale to jest założenie którego nie może przyjąć.
18 gru 13:49
Tadeusz:
"zauważysz" to miałem na myśli nie z rysunku tylko wykazanie, że ....
18 gru 13:55
salamandra: A co ma na celu przyrównanie przez Jerzego dwóch równań okręgu?
18 gru 15:40
Jerzy:
To porównanie odległości. Odległość A od S jest taka sama jak B od S.
18 gru 15:42
salamandra: Skoro ta odległość to jest tak naprawdę prosta(odcinek), to dlaczego stosujemy równanie okręgu?
18 gru 15:44
Blee:
zauważ, że:
1) wyznaczył wzór ogólny okręgu:
(x1 − (y−2))2 + (x2 − y)2 = r2 ze względu na to że środek okręgu leży na prostej x =
y−2
2) następnie podstawił współrzędne punktów które mają należeć do okręgu, więc:
(3 − (y−2))2 + (0 − y)2 = r2
(−1 − (y−2))2 + (2 − y)2 = r2
3)
i przyrównuje lewe strony
18 gru 15:46
Jerzy:
Korzystamy ze wzoru na odległość dwóch punktów i porównujemy je ze sobą.
To co napisałem, to już po podniesieniu obu stron równania do kwadratu, stąd nie ma już
pierwiastków.
18 gru 15:48
salamandra: Brakowało mi tego "r",
czyli po wyliczeniach wyjdzie mi, że y = 5, więc S(3,5) i żeby obliczyć promień, to mogę jakoś
ten wyliczony "y" wstawić do któregoś z równań? Wychodzi mi równanie tożsamościowe jak wstawię
18 gru 15:52
salamandra: Rozumiem Jerzy, właśnie chciałem spytać dlaczego nie korzystamy ze wzoru na odległość dwóch
punktów, nie zauwazylem tego podniesienia do kwadratu
18 gru 15:53
salamandra: Ok, co do tego z 15:52 już wiem, po prostu zamiast pod jedno wstawić "y", a po prawej zostawić
r2, wstawiałem do (y − 2 − 3)2 + (y − 0)2 = (y − 2 + 1)2 + (y − 2)2
18 gru 15:56
salamandra: Teraz mam problem z trudniejszym przykładem:
b) przechodzącego przez punkt P(1,0), stycznego do prostych okreslonych równaniami:
1) x+y−2 = 0
2) x+y+3 = 0
Zauważam, że są to proste równoległe, więc odległość między nimi to średnica okręgu.
| | 25 | |
Po obliczeniach wychodzi mi, że promień to |
| (dobrze, sprawdziłem). |
| | 8 | |
Wziąłem punkt leżący na pierwszej prostej M(2,0), i obliczyłem odległość tego punktu od prostej
ze wzoru:
https://matematykaszkolna.pl/strona/1249.html
Natomiast teraz nie wiem jak wyznaczyć środek, wiem, że prawdopodobnie będą dwa, bo ten punkt
P(1,0) może być zarówno po lewej stronie okręgu jak i prawej, zależy od środka.
Prosiłbym o wskazówkę, nie o rozwiązanie, gdyż chciałbym to zrobić sam, ale zatrzymałem się w
tym miejscu i nie wiem co dalej.
18 gru 16:00
Mila:
Podpowiedź:
1) Środek okręgu leży na prostej równoległej do obu prostych,
jednakowo odległej od obu prostych.
18 gru 16:37
salamandra: Czyli, jak wziąłem sobie ten punkt M(2,0), to biorę punkt N leżący na drugiej prostej, leżący
na x = 2, czyli N(2,−5), w związku z tym, współrzędna "y" środka musi być równa −2,5?
18 gru 16:39
Mila:
Tak, napisz teraz równanie prostej :
| | 5 | |
y=−x+b i przechodzącej przez (2,− |
| ) |
| | 2 | |
Prościej środek odcinka dla punktów A=(0,2) i (B=(0,−3)
18 gru 17:06
salamandra: | | |C1−C2| | |
a dlaczego jest wzór na odległość między prostymi równoległymi d = |
| , w |
| | √A2+B2 | |
tym momencie to odległość między tymi prostymi (1 oraz 2) nie wychodziłaby 5.
18 gru 17:08
salamandra:
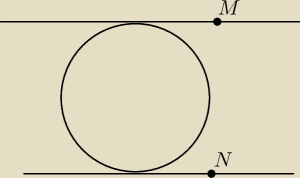
| | 5√2 | |
Odległość między prostymi to |
| , a jakby liczyć z odległości dwóch punktów, to |
| | 2 | |
wychodzi 5.
18 gru 17:11
Mila:
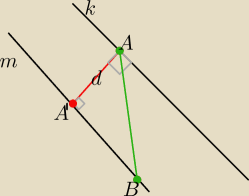
Odległość między prostymi to długość odpowiedniego odcinka prostopadłego ;
d=|AA'|− odległość między prostymi.
|AB|− odległość między punktami
AB nie jest prostopadłe do k i do m
18 gru 17:24
Mila:
Przez środek AA' a także przez środek AB będzie przechodziła prosta równoległa do obu prostych
i jednakowo odległa od nich.
18 gru 17:26
salamandra: aha, a ja właśnie myślałem, że AB jest prostopadłe, ale to miałoby tylko zastosowanie, gdy
prosta by była określona równaniem y=−5 oraz y = 0, racja?
| | 1 | |
Obliczyłem równanie prostej: y = −x− |
| , ale nadal nie wiem jak wyznaczyć współrzędne |
| | 2 | |
środka
18 gru 17:28
salamandra: Współrzędne środka (a, −2,5), więc odległość od punktu P(1,0) do tej prostej musi być równy
promienowi?
18 gru 17:36
Mila:
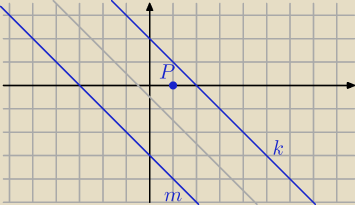
| | 1 | | 1 | |
Środek okręgu należy do prostej y=−x− |
| ⇔O=(a, −a− |
| ) |
| | 2 | | 2 | |
| | 25 | |
Okrąg ma środek O , r2= |
| i przechodzi przez P=(1,0) |
| | 8 | |
18 gru 17:53
Saizou :
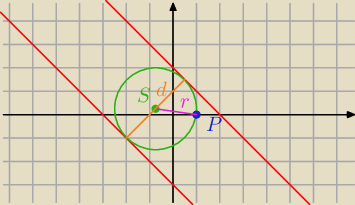
K1
Tip: S leży na prostej równoległej do prostej l
1 oraz l
2
Cel: napisanie tej prostej
K2
| | 1 | |
Tip: r= |
| d d− odległość między l1 a l2 |
| | 2 | |
Cel: wyznaczenie długości promienia okręgu
K3
Tip: |SP|=r
Cel: wyznaczenie współrzędnych punktu S
K4
Cel: zapisanie równania okręgu (będą dwa takie okręgi)
18 gru 17:56
salamandra: Dziękuję Wam, jeszcze dopytam, bo nie mogę tego zrozumieć, np. w pierwszy wpisie Jerzego, lub
Mili, z tymi współrzędnymi środka, że np.
S(y−2, y) [wpis Jerzego], jak do tego dojść?
18 gru 18:13
Saizou :
Skoro punkt leży na prostej, to spełnia jej równanie
np.
Niech punkt K leży na prostej o równaniu y=2x+3.
Ogólnie punkt K ma współrzędne (x, y), ale wartość y możemy doliczyć przy pomocy wzoru prostej,
czyli mam K = (x, 2x+3))
18 gru 18:16
salamandra: Czyli skoro S(x,y), a x= y−2, to S(y−2, y) i robimy to po to, aby mieć tylko jedną niewiadomą?
18 gru 18:17
Saizou :
Dokładnie tak

18 gru 18:17
salamandra: Tylko tutaj jest trochę w odwrotną stronę niż normalnie

18 gru 18:18
Saizou :
@Jerzy wybrał tę opcję, żeby nie mieć ułamków

@Mila wybrała standardową opcję
18 gru 18:20
salamandra: I w końcu nie wiem, czy Jerzy zastosował wzór na odległość dwóch punktów, czy tak jak Blee
mówi, układ równań z dwoma równaniami okręgu, bo jeśli założyłbym, że to odległość dwóch
punktów, to
AS=BS.
AS= √(y−2−3)2+(y−0)2
BS = √(y−2+1)2+(y−2)2
AS = BS
y=5
S(3,5), i w tym momencie powinienem wyliczyć r ze wzoru √a2+b2−c z postaci ogólnej okręgu?
18 gru 18:27
Jerzy:
(AS)2 = (BS)2 i znikają pierwiastki.
18 gru 18:31
Saizou :
@Jerzy bardzo skrótowo opisał swoją metodę

@Blee ją uszczegółowił.
PS. niezależnie jaką metodę wybierzesz, ważne żeby wszystko co robisz było zgodne z prawami
matematyki
18 gru 18:31
salamandra: Wiem, ja to policzyłem i wyliczyłem środek, ale jak dojść do promienia?
18 gru 18:31
Saizou :
Zobacz na mój post z opisanymi krokami
18 gru 18:32
salamandra: w b) już wiem o co chodzi, na chwilę wróciłem do tego a), bo teraz dopiero wszystko notuję.
18 gru 18:33
Jerzy:
Skoro masz współrzędne S , to promień jest odległością A od S lub B od S.
18 gru 18:33
Feng Si Niang:
18 gru 18:34
salamandra: no tak, czyli teraz po prostu wstawiam do jednego z nich (AS lub BS) otrzymane y, nie wiem
dlaczego tego nie widzę
18 gru 18:35
Jerzy:
Liczysz odległość punktu A od S.
18 gru 18:36
salamandra: Już wiem, wyszło, dzięki, pewnie się tu za niedługo odezwę, bo podejrzewam, że c) będzie
trudniejszy.
18 gru 18:38
Saizou :
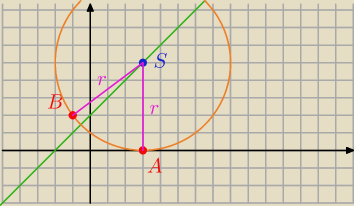
Napisz równanie okręgu przechodzącego przez punkty A i B gdzie A(3,0), B(−1, 2)
Którego środek leży na prostej o równaniu x−y+2=0.
S=(x, x+2)
|SB|=|SA|
Z tego masz współrzędne punktu S
r = |SA|
18 gru 18:40
Mila:
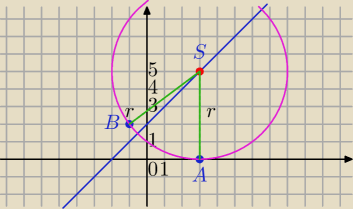
Trzeba wykonać rysunek, to jest geometria.
a)
A(3,0), B(−1, 2)
S=(a,b) − środek okręgu
(x−a)
2+(y−b)
2=r
2− równanie okręgu
1) środek okręgu należy do prostej :
k: x−y+2=0⇔y=x+2
S=(a,b) − wsp. spełniają równanie y=x+2⇔
S=(a,a+2)
|SA|=|SB|⇔
√(3−a)2+(0−a−2)2=
√(−1−a)2+(2−a−2)2 /
2 itd
a=3
S=(3, 5) i A=(3,0) mają jednakowe wsp x−owe to :
2) długość promienia:
r=|SA|=|5−0|=5
To samo wyjdzie z rachunku:
r=|SB|=
√(3+1)2+(2−5)2=
√16+9=
√25=5
(x−3)
2+(y−5)
2=25
==========================
18 gru 19:02
salamandra:
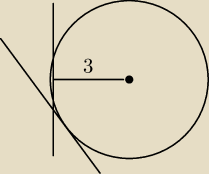
Teraz mam podane, że okrąg jest styczny do osi y i prostej o równaniu y=−x oraz jego promień
wynosi 3
Co powinienem najpierw z tych danych wyciągnąć?
18 gru 20:15
salamandra: Skoro jest styczny do osi y i jego promień jest równy 3, to na pewno jest też styczny do
prostej o równaniu x=6 lub x=−6 (?)
18 gru 20:18
Jerzy:
Pierwszy wniosek: S = (3,y)
18 gru 20:32
salamandra: No właśnie do tego doszedłem. Potem wzorem na odległość środka od prostej y= −x, która musi się
równać promieniowi?
18 gru 20:38
Jerzy:
Dokładnie.
18 gru 20:51
salamandra: wyszły mi dwa rozwiązania, a powinny wyjść cztery:
wyszło mi:
S(3,y)
| | |1*3+1*y| | | |3+y| | |
d= |
| = |
| = 3 |
| | √2 | | √2 | |
| 3+y | | 1 | | 3+y | | 1 | |
| = 3 * |
| v |
| = −3 / * |
| |
| √2 | | √2 | | √2 | | √2 | |
| 3+y | | 3 | | 3+y | | −3 | |
| = |
| v |
| = |
| |
| 2 | | √2 | | √2 | | √2 | |
| 3+y | | 3√2 | | 3+y | | −3√2 | |
| = |
| /*2 v |
| = |
| /*2 |
| 2 | | 2 | | 2 | | 2 | |
3+y = 3
√2 v 3+y = −3
√2
y= 3
√2−3 v y= −3
√2−3
18 gru 20:58
salamandra: Aha, teraz muszę rozważyć przypadek, gdy S(−3,y)?
18 gru 21:00
Mila:
Tak .
18 gru 21:09
Mila:
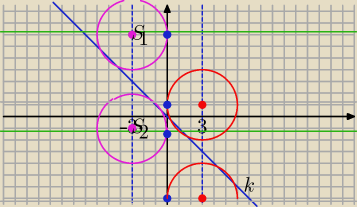
k: y=−x
1) Promień jest prostopadły do OY w punkcie styczności .
środek okręgu leży na prostej x=−3 lub x=3
S=(−3,b) lub x=(3, b)
2) odległość S od prostej x+y=0 jest równa 3
| | |−3+b| | |
d(S,k)= |
| =3 i S=(−3,b) |
| | √2 | |
|b−3|=3
√2
b−3=3
√2 lub b−3=−3
√2⇔S=(−3,3+3
√2
b=3+3
√2 lub b=3−3
√2⇔S=(−3,3−3
√2)
S=(3,b)
|b+3|=3
√2
b+3=3
√2 lub b+3=−3
√2⇔
b=−3+3
√2 lub b=−3−3
√2⇔
S=(3,−3+3
√2) lub S=(3,−3−3
√2)
18 gru 21:10
salamandra: A dlaczego w ogóle liczymy odległość od prostej x+y=0, a nie od prostej x=0? Przecież to też 3
18 gru 21:13
Jerzy:
Bo jest nieskończenie wiele okręgów o promieniu r = 3 stycznych do prostej x = 0 (czyli osi OY)
18 gru 21:41
Mila:
Liczysz odległość od prostek y=−x , bo okrąg ma być do niej styczny,
ponadto ustalono, że środek okręgu należy do prostej x=−3 lub x=3 i to już ustala odległość od
OY.
18 gru 21:59
Mila:
Prosta x=0 to y∊R i co policzysz?
18 gru 22:09
salamandra: Dziękuję za pomoc

18 gru 22:17
Mila:
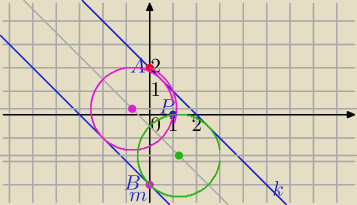
zadanie 1)
P=(1,0)
k: x+y−2 = 0⇔y=−x+2
m: x+y+3 = 0⇔ y=−x−3
1) Środek okręgu leży na prostej równoległej do obu prostych, jednakowo odległej od obu
prostych
a) Piszemy równanie prostopadłej do obu prostych i przechodzącej przez punkt ∊k
np. A= (0,2) ( tak będzie najprościej )
y=x+2
b) Punkt przecięcia z prostą m:
x+2=−x−3
środek AB
prosta s ||k i s||m S∊S
2) Odległość prostych równoległych z równań ogólnych:
| | |−2−3)| | | 5√2 | |
d(k,m)= |
| = |
| |
| | √2 | | 2 | |
− długość średnicy okręgu:
| | 1 | |
3)O=(a, −a− |
| ) ,P= (1,0) |
| | 2 | |
lub
| | 3 | | 1 | | 5 | | 7 | |
O1=(− |
| , |
| ), lub O2=( |
| , − |
| ) |
| | 4 | | 4 | | 4 | | 4 | |
Zostają równania.
18 gru 22:19
salamandra: Dziękuję Milu jeszcze raz za wysiłek, chociaż wątpię, aby miał on miejsce

18 gru 22:26


 Odległość między prostymi to długość odpowiedniego odcinka prostopadłego ;
d=|AA'|− odległość między prostymi.
|AB|− odległość między punktami
AB nie jest prostopadłe do k i do m
Odległość między prostymi to długość odpowiedniego odcinka prostopadłego ;
d=|AA'|− odległość między prostymi.
|AB|− odległość między punktami
AB nie jest prostopadłe do k i do m

 K1
Tip: S leży na prostej równoległej do prostej l1 oraz l2
Cel: napisanie tej prostej
K2
K1
Tip: S leży na prostej równoległej do prostej l1 oraz l2
Cel: napisanie tej prostej
K2


 @Mila wybrała standardową opcję
@Mila wybrała standardową opcję
 @Blee ją uszczegółowił.
PS. niezależnie jaką metodę wybierzesz, ważne żeby wszystko co robisz było zgodne z prawami
matematyki
@Blee ją uszczegółowił.
PS. niezależnie jaką metodę wybierzesz, ważne żeby wszystko co robisz było zgodne z prawami
matematyki
 Napisz równanie okręgu przechodzącego przez punkty A i B gdzie A(3,0), B(−1, 2)
Którego środek leży na prostej o równaniu x−y+2=0.
S=(x, x+2)
|SB|=|SA|
Z tego masz współrzędne punktu S
r = |SA|
Napisz równanie okręgu przechodzącego przez punkty A i B gdzie A(3,0), B(−1, 2)
Którego środek leży na prostej o równaniu x−y+2=0.
S=(x, x+2)
|SB|=|SA|
Z tego masz współrzędne punktu S
r = |SA|
 Trzeba wykonać rysunek, to jest geometria.
a)
A(3,0), B(−1, 2)
S=(a,b) − środek okręgu
(x−a)2+(y−b)2=r2− równanie okręgu
1) środek okręgu należy do prostej :
k: x−y+2=0⇔y=x+2
S=(a,b) − wsp. spełniają równanie y=x+2⇔
S=(a,a+2)
|SA|=|SB|⇔
√(3−a)2+(0−a−2)2=√(−1−a)2+(2−a−2)2 /2 itd
a=3
S=(3, 5) i A=(3,0) mają jednakowe wsp x−owe to :
2) długość promienia:
r=|SA|=|5−0|=5
To samo wyjdzie z rachunku:
r=|SB|=√(3+1)2+(2−5)2=√16+9=√25=5
(x−3)2+(y−5)2=25
==========================
Trzeba wykonać rysunek, to jest geometria.
a)
A(3,0), B(−1, 2)
S=(a,b) − środek okręgu
(x−a)2+(y−b)2=r2− równanie okręgu
1) środek okręgu należy do prostej :
k: x−y+2=0⇔y=x+2
S=(a,b) − wsp. spełniają równanie y=x+2⇔
S=(a,a+2)
|SA|=|SB|⇔
√(3−a)2+(0−a−2)2=√(−1−a)2+(2−a−2)2 /2 itd
a=3
S=(3, 5) i A=(3,0) mają jednakowe wsp x−owe to :
2) długość promienia:
r=|SA|=|5−0|=5
To samo wyjdzie z rachunku:
r=|SB|=√(3+1)2+(2−5)2=√16+9=√25=5
(x−3)2+(y−5)2=25
==========================
 Teraz mam podane, że okrąg jest styczny do osi y i prostej o równaniu y=−x oraz jego promień
wynosi 3
Co powinienem najpierw z tych danych wyciągnąć?
Teraz mam podane, że okrąg jest styczny do osi y i prostej o równaniu y=−x oraz jego promień
wynosi 3
Co powinienem najpierw z tych danych wyciągnąć?
 k: y=−x
1) Promień jest prostopadły do OY w punkcie styczności .
środek okręgu leży na prostej x=−3 lub x=3
S=(−3,b) lub x=(3, b)
2) odległość S od prostej x+y=0 jest równa 3
k: y=−x
1) Promień jest prostopadły do OY w punkcie styczności .
środek okręgu leży na prostej x=−3 lub x=3
S=(−3,b) lub x=(3, b)
2) odległość S od prostej x+y=0 jest równa 3

 zadanie 1)
P=(1,0)
k: x+y−2 = 0⇔y=−x+2
m: x+y+3 = 0⇔ y=−x−3
1) Środek okręgu leży na prostej równoległej do obu prostych, jednakowo odległej od obu
prostych
a) Piszemy równanie prostopadłej do obu prostych i przechodzącej przez punkt ∊k
np. A= (0,2) ( tak będzie najprościej )
y=x+2
b) Punkt przecięcia z prostą m:
x+2=−x−3
zadanie 1)
P=(1,0)
k: x+y−2 = 0⇔y=−x+2
m: x+y+3 = 0⇔ y=−x−3
1) Środek okręgu leży na prostej równoległej do obu prostych, jednakowo odległej od obu
prostych
a) Piszemy równanie prostopadłej do obu prostych i przechodzącej przez punkt ∊k
np. A= (0,2) ( tak będzie najprościej )
y=x+2
b) Punkt przecięcia z prostą m:
x+2=−x−3
