romby salamandra: Stosunek długości przekątnych rombu jest równy 1:4. Oblicz miarę kąta ostrego α tego rombu.

	α		1
tg		=
	2		4

	α
t=
	2

	1
tg t =
	4

t ≈ 14 stopni

	α
14 stopni =		/ * 2
	2

28 stopni = α Czy dobrze to rozwiązałem? Jest jakiś sposób żeby rozwiązać to wyjściowe równanie

	α
trygonometryczne bez podstawiania t? (aby zamienić		na α?)
	2

ICSP:

	x   2tg( )   2
sinx =
	x   tg2( ) + 1   2

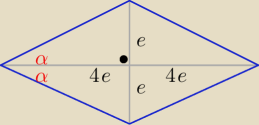
a@b: tgα=1/4

	2tgα
tg(2α)=		=.......... = 8/17
	1+tg2α

ICSP: Eta minus w mianowniku.

salamandra:

	1   2*   4		1		16		8
sinx =		=		*		=
	1   2 + 1 4		2		17		17

	8
sinx =		≈ 0,4705
	17

28 stopni = 0,4695 x≈ 28

salamandra: A jak mam zadanie, żeby wykazać, że pole P równoległoboku o bokach a i b oraz kącie ostrym α między nimi, określone jest wzorem P = ab*sinα to wystarczy, że powiem, że przekątna podzieli ten równoległobok na dwa trójkąty o bokach a,b i kącie α między nimi zawartym. W związku z tym, że mamy dwa takie trójkąty, a wzór na pole trojkąta o bokach a,b i kącie między nimi zawartym to 1/2*a*b*sinα to pole równoległoboku to 2*1/2*a*b*sinα więc = absinα?

a@b: tak

salamandra: Tak w ogóle, dlaczego przekątne równoległoboku nie przecinają się pod kątem prostym, a rombu tak?

a@b:

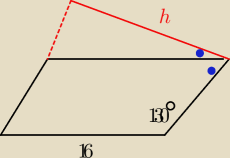
salamandra: Udowodnij, że można (lub nie można) obliczyć drugi bok równoległoboku ABCD Pierwsze w sumie zasadnicze pytanie, czy kąty zaznaczone kropkami będą równe? Bo jak tak, to są one równe 50 stopni, ale co dalej?

Mila: Napisz pełną treść zadania.

ICSP: Znowu to zadanie. https://matematykaszkolna.pl/forum/394958.html Bok BC można ustalić dowolnie, więc pole nie jest określone jednoznacznie. Długość h jak i pole trójkąta można natomiast obliczyć, ale pytanie jest o pole równoległoboku.

salamandra: Nie, polecenie w zadaniu to wyznaczyć wysokość. A dodatkowe zadanie to to o którym napisałem, nie ma nic o polu.

salamandra: Polecenie: Uwzględnij dane przedstawione na rysunku, gdzie czworokąt ABCD jest równoległobokiem i oblicz długość jego wyskości h. Wynik zaokrąglij do 0,1. Dodatkowe polecenie od nauczyciela: Udowodnij, że można (lub nie można) obliczyć drugi bok równoległoboku ABCD. Wysokość wiem jak policzyć, ale tego dodatkowego nawet nie wiem jak ruszyć. Domyślam się, że nie można go obliczyć, bo tę prostą BC można ciągnąć w nieskończoność, ale jak to udowodnić

salamandra: A, zapomniałem dodać, że nauczyciel zasugerował użycie jakiegoś kontrargumentu, więc jak powiem, że bok BC można wydłużyć w nieskończoność i nie zmienią się wartości h, ani żadne z kątów, więc de facto go nie znamy, to wystarczy?

a@b: tak