Całka podwójna kasia: Oblicz objętość bryły ograniczonej płaszczyznami: x²+y²+1=z, √5−x²−y² = z. Widzę to przecięcie, i wiem, że muszę zrzutować na oś XOY okrąg, który będzie moim obszarem całkowania, jednak nie potrafię wyliczyć jego równania.

kasia: powierzchniami* w poleceniu.

kasia: czy to będzie x²+y²=2?

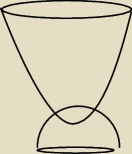
a7: mamy paraboloidę x²+y²=z−1 oraz kulę x²+y²+z²=5

kasia: Tak.

a7: paraboloida ma wierzchołek w x=0 y=1 z=0 kula ma promień √5 x²+y⁺z²−5=x²+y²−z+1 z²+z−6=0 Δ=25 √Δ=5 z₁=−2 z₂=2 r okręgu przecięcia równe 2, chyba tak jak napisalaś ? czyli obszar −2≤x≤2 1≤y≤√5 −2≤z≤2 i robimy całkowanie podwójne czy potrójne

kasia: Całkowanie podwójne. Potem porownalam y² z oby równań. I wyszedł mi okrąg x²+y²=1. Więc już całkiem zglupialam

kasia: z nie mogą być ujemne, bo działamy nad powierzchnią XOY

kasia: Ale w programie, gdzie to rysowałam, obszarem nie był okrąg o promieniu 1, tylko większym

a7: okrąg ma promień 2 to mimo wszystko raczej chyba na pewno sensowne

a7: ?

a7: zajrzyj tu https://matematykaszkolna.pl/forum/203665.html

a7: https://forum.zadania.info/viewtopic.php?f=37&t=38912

a7: √5−x2−y2 = z to półsfera

kasia: W odp. jest błąd. Objętość z odp. to objętość pod samą półsferą. Obszar będzie okręgiem o promieniu 1, w środku (0,0).

kasia: Wystarczy podstawić z=2 do obu równań.

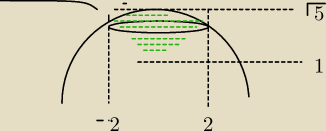
a7: nie, Kasia zobacz mój rysunek (kreska z lewej u góry robi się sama i nie należy do rysunku)

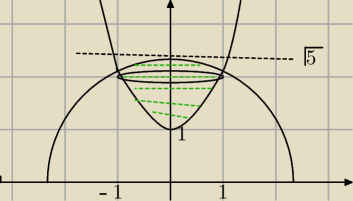
a7: w pierwszym linku było że ten promień jest jednak 1

a7: promień jest równy 1 (liczymy ze współrzędnych biegunowych) patrz link nr2

kasia: Promień będzie równy 1. Sprawdziłam to rachunkowo i na rysunku w programie graficznym. Plus odpowiedź wychodzi mi taka, jaka powinna

a7: no to wszystko ok, tak?