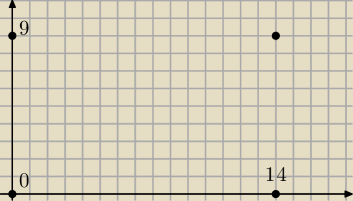
kombinatoryka, krata, ilosc ruchow student: Ile jest dróg z punktu A = (0,0) do B=(14,9) a.) jeżeli w każdym ruchu można się poruszyć o jedną jednostkę w prawo lub w górę? b.) jeżeli w każdym ruchu można się poruszyć również po przekątnej ( jednocześnie w prawo i w górę) ?

student:

	21!		21 13		21 9
a.) rozwiazalem i jest		=		=		mozliwych dróg
	13!9!

umiałby ktoś wytłumaczyć co zrobić z tymi przekątnymi?

a7:

a7: w 14 krokach najkrócej pokonujemy odległość jeśli pójdziemy po przekątnej (9 po przekątnej plus 5 po prostej), więc i pewnie wystarczy 'spermutować' i podzielić na tej samej zasadzie co w a)

student: Takich przekątnych ( prawo i góra ) jest tyle ile jest kwadracików w tym "prostokącie" czyli 13*9=117 , a maksymalna ilość ruchów po przekątnej to 8, czyli mogę zrobić ciąg składający się z −1,0,1 odpowiednio(prawo,góra,przekatna) i bedzie 13+8+8=29 elementow w ciagu i dzielę przez permutację każdego takiego wystapienia ponieważ −1,0,1 są nie rozróżnialne same z sobą tak samo jak ruchy ?

	29!
wyszłoby mi
	13!8!8!

a7: maksymalna ilość ruchów po przekątnej to 9?

student:

	30!
oups 9 ruchów po przekatnej ... byloby		, ale w zadaniu nie chodzi o najkrótszą
	13!8!9!

drogę tylko o ilość możliwych dróg czyli mogę się w ogóle nie poruszyć po przekatnej

a7: ilość możliwych dróg bez cofania się rozumiem, a masz odpowiedzi?

student: tylko ... sposób z ciągiem jest chyba nieprawidłowy bo jak poruszę się 9 razy po przekątnej to zostaną mi jeszcze 5 ruchow w prawo, czyli ciag skladajacy sie z 14 elementow ...

student: nie mam odpowiedzi a w internecie co znalazlem to przyklady z krata gdzie mozna tylko w bok i w górę które są proste

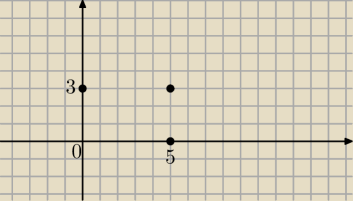
a7: może trzeba spróbować na prostym przykładzie np A(0,0) i B(5,3)

a7: dodajemy "zwykłe" drogi plus "ukośne"

a7: w tym prostszym przykładzie widać, że chodzi o to żeby 5 ruchów zrobić z czego 3 są ZAWSZE ukośne a dwa zawsze płaskie

student: a gdyby z punktu (0,0) mieć 3 mozliwosci ruchu i tak rekurencyjnie dalej ?

a7: czyli na ile sposobów możemy wybrać dwa rodzaje ruchów tak żeby w sumie ich było pięć z czego jednego zawsze jest trzy a między nim 2 inne w dowolnych miejscach

student: twój sposób mysle ze by dzialal gdyby mozna tylko w bok i po ukosie sie poruszac bo nie ma innej mozliwosci dostania sie do B jak nie 3 po ukosie 2 w bok

a7: https://matematykaszkolna.pl/forum/351545.html

student: ooo mam chyba pomysł : jak oznaczymy 0 −> ruch w prawo , 1 −> ruch w góre to zalozmy ciag 01001010 , gdy 01 lub 10 jest kolo siebie to znaczy ze poruszylismy sie po ukosie czyli

	7 3
traktujemy jako jeden ruch, to liczba sposobow rozmieszczenia 01 w 8−1 miejsach to		* 2

(bo 10 tez moze byc i moga byc tylko 3 przekatne w ciagu) czyli 90 sposobow ?

a7: z tego co pisze Adamm wynika mi, choć nie wiem czy dobrze zrozumiałam że jak już pisałam ja sumujemy drogi zwykłe plus drogi na skos drogi na skos to tak jakby droga do góry czyli jakby krata miała mniejszy wymiarmamy w Twoim przypadku czternaście kroków dziewięć do góry wybieramy więc z 14 9 i nie wiem co dalej i wybieramy je na 5! sposobów

student: jak pojdziemy 9 po przekatnej to zostanie 5 ruchow w bok ktore mozemy wykonac w kazdym momencie

	(9+5)!
to moze bedzie to
	9!5!

student:

	21 13		14 9
czyli wynik koncowy zadania bedzie		+

student: tylko znowu mi cos nie pasuje bo wcale nie musimy wykonywac maksymalnej ilosci ruchow po przekatnej, a tym wyniku przypadkow kiedy pojdziemy po przekatnej 3 razy , w bok 10 razy i w gore 5 razy nie liczymy, przynajmniej mi sie tak wydaje

a7: http://www.deltami.edu.pl/temat/matematyka/kombinatoryka/2013/12/31/Drogi_w_kratach_i_kino/

	14 5
dróg po przekątnej będzie		(patrz analogia do wytłumaczenia dla zadania 1 w linku)

student:

14 5
	to liczba gdy pojdziemy 9 razy po przekatnej i 5 razy w bok

a7: no tak teraz jeszcze tylko prawidłowo określi liczbę zwykłych dróg

23 14

a7: eidt : *określić

Pytający:

	23 9		23 14
a) 14+9=23 Znaczy odpowiedzią jest		=		.

b) Może najpierw rozważ sobie, że wykonujesz dokładnie 1 ruch na ukos. Wtedy będziesz miał do wykonania o 1 ruch w prawo mniej i o 1 ruch w górę mniej. Znaczy będziesz miał 14−1=13 ruchów w prawo, 9−1=8 ruchów w górę i 1 ruch na ukos. Różnych kolejności tych ruchów jest

	((14−1)+(9−1)+1)!		(14−1)+(9−1)+1 1		(14−1)+(9−1) (9−1)
		=		*		.
	(14−1)!*(9−1)!*1!

Analogicznie dla 2, 3, ..., 9 ruchów na ukos. Stąd rozwiązaniem jest:

	((14−k)+(9−k)+k)!		(23−k)!
∑k=09		= ∑k=09		.
	(14−k)!*(9−k)!*k!		(14−k)!*(9−k)!*k!

student:

	23 14
a no tak w kracie w a.) jest		pomylilo mi sie z przecznicami gdzie trzeba na poczatku

odjąć po 1 z kazdej strony

student: bardzo dobre rozwiazanie dzieki