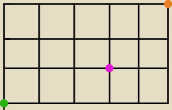
kombinatoryka ola: Jaka jest liczba najkrótszych dróg, prowadzących po bokach kwadratów od punktu A do punktu B przez punkt E? punkt A jest zielony punkt E jest różowy punkt B jest pomarańczowy i wszystkie kratki są równej długości

Adamm: wszystkie najkrótsze drogi od A do E + wszystkie najkrótsze drogi od E do B

	1+3 1		2+2 2
zatem mamy		+		=10 dróg

ola: właśnie, że 24 a sama licząc na piechotę i grupując różne przypadki doliczyłam się 16

Pytający: Wypadałoby raczej pomnożyć.

	1+3 1
A do E na		=4 sposoby

	2+2 2
E do B na		=6 sposobów

A do B przez E na 4*6=24 sposoby.

Adamm: faktycznie, moja wina

ola: A jak wymyśliliście te kombinacje?

ola: bo ja tego nie widzę

Adamm: załóżmy masz szachownicę m x n żeby przejść najkrócej, musisz wykonać n+m ruchów wybierasz jedynie kiedy zmienić kierunek, dlatego z n+m musisz wybrać n miejsc w których go zmieniasz (lub odpowiednio m miejsc, to to samo)

	n+m m
dlatego mamy		sposobów

Adamm: "wybierasz jedynie kiedy zmienić kierunek" raczej kiedy idziesz do góry, lub odpowiednio na bok

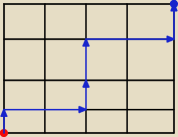
Adamm: przykład, mamy szachownicę 4 x 4 startując z czerwonego punktu chcemy policzyć na ile sposobów można przejść do niebieskiego jedyne co musimy wybrać, to w których punktach iść na górę myśl o tym jak o sekwencji ruchów mamy załóżmy x oraz y jako odpowiednie ruchy musimy położyć 4 iksy oraz 4 igreki w odpowiedniej kolejności, zdecydować się w jakiej kolejności mają się znajdować np. x, y, x, x, y, y, x, y zadanie sprowadza się do wyboru miejsc

Adamm: nie wiem czy to jest jasne, starałem się wyjaśnić o co chodzi

ola: Już rozumiem, jeśli x to ruch do góry a y to ruch w prawo to w moim zadaniu mam x,y,y,y i x,x,y.y, w dowolnej kolejności wiec ilosc zdarzeń to iloczyn dwóch wariacji z powtórzeniami równy 24

Adamm: myślę że nie rozumiesz tutaj mamy 1 x 3 oraz 3 x 5 dla 1 x 3 musimy przejść 4 kroki zatem mając [ ] [ ] [ ] [ ] wybieramy z 4 pustych miejsc 3 na których kładziemy kroki w prawo, a w resztę wstawiamy kroki w górę

	4 1		4!
zatem mamy kombinację		=
			(4−3)!*1!

podobnie robimy dla 3 x 5

Adamm:

	n k
kombinacja		to wybór grupy k−elementowej z grupy n−elementowej

tutaj grupa n−elementowa to puste miejsca, a grupa k−elementowa to miejsca na których ustawiamy kroki w prawo

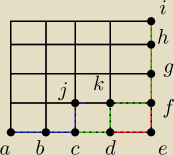
PrzyszlyMakler: Adamm, zadania z drogami są dla mnie bardzo trudne i nie potrafię ich zrozumieć, a próbowałem wiele razy, więc może spróbujesz mi to wytłumaczyć raz jeszcze. Bo pisałeś, że wystarczy policzyć ile jest możliwości ruchu do góry, ale przecież droga przechodząca przez punkty abcdefghi (1) droga, a juz droga abcdkfghi to juz inna opcja, tak samo jak abcjkfghi to dlaczego mówisz ze wystarczy obliczyc tylko ilosc ruchow do góry?

Adamm: ilość ruchów do góry jest zawsze taka sama ważna jest kolejność wykonywanych ruchów

PrzyszlyMakler: Więc jak to obliczyć? :C

Adamm: patrz na swój rysunek wybierasz tylko w jakiej kolejności idziesz, czyli wybierasz kiedy iść na górę a kiedy w prawo, ale ilość kroków w górę, oraz w prawo jest zawsze taka sama wynika to z tego że idziemy najkrótszymi drogami żeby to zrobić musisz wybrać miejsca z 8 (tyle kroków wynosi najkrótsza droga) dla których idziesz na górę (idziesz na górę 4 razy) można to zaprezentować 8 pustymi miejscami w szeregu

	8 4
a takie kroki w górę możesz wybrać na		sposobów

Adamm: czyli problem polega na tym jak wypełnić nierozróżnialne kroki w górę mając ileś pustych miejsc w szeregu (kroki w prawo zostają w pozostałych)

Adamm: |*| |*| |*| załóżmy mamy prostokąt 2 x 1 musimy przejść 2 razy do góry i jeden raz w prawo my musimy zadecydować jedynie kiedy a to sprowadza się do wyboru pustych miejsc z tych 3 pustych miejsc na górze wybieramy 2, a w resztę wstawiamy kroki w prawo

	3 2		3 1
to czysty przypadek kombinatoryczny, miejsca możemy wybrać na		=		=3 sposoby

PrzyszlyMakler: Nie wiem dlaczego, ale drogi wyjątkowo topornie mi idą. Dziękuję za starania, choć definitywnie jeszcze musze do tego przysiąśc. Niby w teroii rozumiem, ale jestem pewien, że bym sobie nie poradził z jakimś typowym zadaniem, że przez ten punkt trzeba przejść/lub nie można.