Geometria płaska
dilloneq:
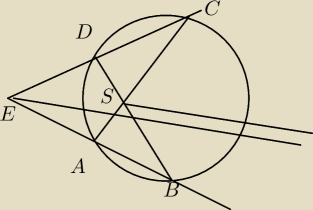
W czworokącie ABCD wpisanym w okrąg przedłużono boki AB i CD aż do przecięcia w punkcie E.
Przekątne AC i BD przecinają się w punkcie S.
Wykaż że dwusieczna kąta BEC jest równoległa do dwusiecznej kąta BSC.
Proszę o pomooc. Zrobiłem to ale na milion kątów, a musi być jakiś czytelniejszy sposób.
9 gru 21:48
a7:
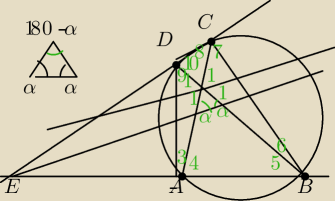
wyszło mi
∡6+∡7+2*∡1=180
o
∡3+∡9+2*∡1=180
o
∡5+∡4+180−2α=180 ⇒ 2α=∡5+∡4
∡8+∡10+180−2α=180 ⇒ 2α=∡8+∡10
∡3+∡9=∡6+∡7=180−2*∡1
∡5+∡4=∡8+∡10=180
o−2∡1
180−2α=180−2*∡1
α=∡1 c.n.w.
============
9 gru 22:32
dilloneq: Dzieki
9 gru 22:47
a7:
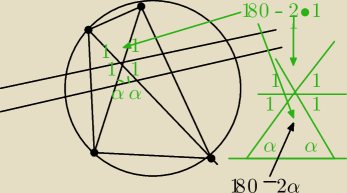
właściwie to od razu widać (na powiększeniu), że 180
o−2∡1=180−2α, α=∡1 c.n.w.
9 gru 22:49
dilloneq: ∡5+∡4=∡8+∡10=180o−2∡1 wytłumaczy mi ktoś tylko z czego to się wzięło
9 gru 22:58
a7:
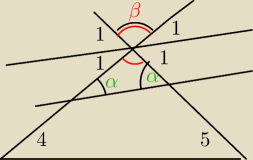
β=180−2*∡1=180−2α ( kąt β jest kątem przyległym do dwóch katów nr 1 więc jest równy
β=180−2*∡1
β jest też kątem wierzchołkowym dla kąta zaznaczonego na czerwono ) suma miar kątów w trójkącie
jest 180, więc β=180−2α
α=∡1 c.n.w.
===========
9 gru 23:06
dilloneq: Rozumiem wszystko tylko, nie wiem dlaczego możemy założyć że te kąty 1 są wszystkie równe.
Wiemy że wierzchołkowe muszą być równe ale dlaczego po drugiej stronie tez jest kąt 1
9 gru 23:10
a7:
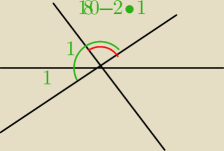
22:58 suma miar kątów w trójkącie jest 180 czyli ∡5+∡4+(180−2*∡1)=180 (180−2*∡1) to jest
miara trzeciego z kątów w ΔABS
wyliczona , gdyż jest to kąt przyległy do dwóch kątów nr 1
9 gru 23:11
dilloneq: Tak to wiem wszystko tylko skąd założenie że tam są dwa równe kąty nr 1
9 gru 23:13
dilloneq: Z czego to wynika, ze nie jest np kąt 1 i 2
9 gru 23:13
a7: bo to przecież dwusieczna tam dzieli kąt na dwa równe kąty (jest to dana z treści zadania)
9 gru 23:13
dilloneq: Boze, dziekuje i sorki
9 gru 23:14
a7: | | 1 | | 1 | |
jeśli mamy dwusieczną to mamy dwa równe kąty i możemy jest oznaczyć |
| α i |
| α, a |
| | 2 | | 2 | |
możemy nr 1 i nr 1
9 gru 23:16
a7: @dilloneq 22:49, rozwiązanie jeszcze krótsze (praktycznie w 1 linijkę plus mogłoby być krótkie
uzasadnienie o kącie przyległym i wierzchołkowym)
9 gru 23:22
dilloneq: a dlaczego ten mały trójkąt jest równoramienny
9 gru 23:22
a7:
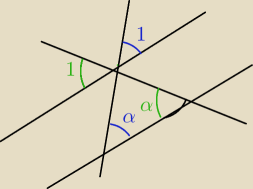
kąty zielone to kąty odpowiadające, a także kąty granatowo−niebieskie to kąty odpowiadające kąt
nr jeden jest równy kątowi nr 1 zielony niebieskogranatowemu więc wszystkie są równe sobie
∡1=
∡1=α
(1)=α
(2)=α
9 gru 23:29
dilloneq: Kocham cie
9 gru 23:30
a7: zaraz zaraz tam chyba rzeczywiście należało oznaczyć na początku α1 i α2
9 gru 23:41
a7: ok już chyba mam
10 gru 00:03
dilloneq: czyli jak to będzie
10 gru 00:04
a7: myślę
10 gru 00:12
dilloneq: <3
10 gru 00:15
a7: 2*∡1=α1+α2 czyli trzeba wykazać, że α1=α2
10 gru 00:20
10 gru 00:21
a7:
10 gru 00:28
dilloneq: a to też jest prawidłowe ? czy tylko z tego linku
10 gru 00:38
a@b:
też dobre
10 gru 00:39
dilloneq: Dziekujee
10 gru 00:44